
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher [261] |
The diagram shows an isosceles triangle (not drawn to scale).

Angle ABC = angle ACB, AB = \(3x+8\) and AC = \(5x-7\).
Use an algebraic method to find the value of \(x\).
2. | GCSE Foundation [333] |
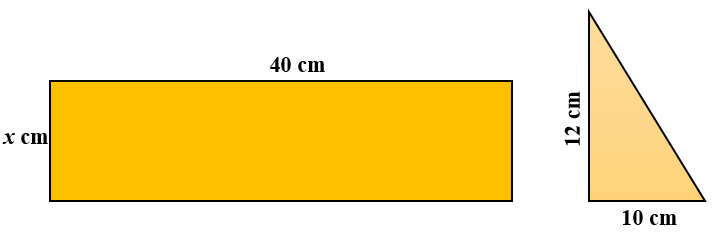
The diagrams show a triangle and a rectangle (not drawn to scale).
The area of the rectangle is six times larger than the area of the triangle. Find the value of \( x \)
3. | GCSE Higher [164] |
The perimeter of the triangle is the same length as the perimeter of the square.
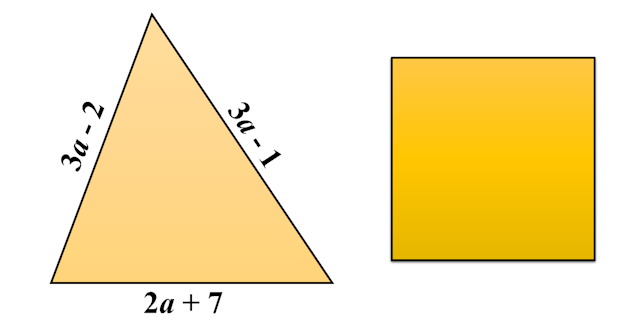
Find an ex
4. | GCSE Higher [143] |
Aimee, Natasha and Ruby play hockey.
If altogether they have scored 35 goals, how many goals did they each score?
5. | GCSE Higher [188] |
Luke, Leia and Han swim lengths of a swimming pool to raise money for charity.

How many lengths did each person swim?
7. | GCSE Higher [331] |
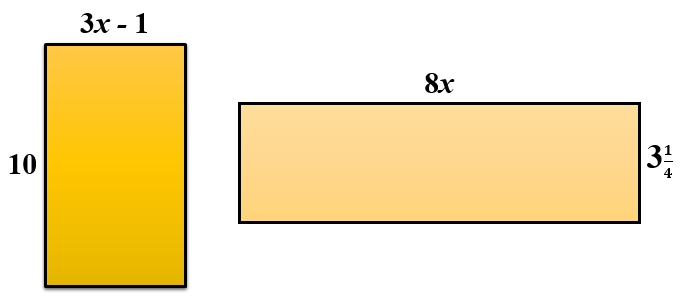
Two rectangles, not drawn to scale, are shown below. All measurements are in centimetres. Both rectangles have the same areas. Work out the perimeter of the rectangle on the left.
9. | GCSE Higher [332] |
The area of rectangle PQRS (not to scale) is 80cm2.
(a) Show that \( x^2 + 14x = 40\).
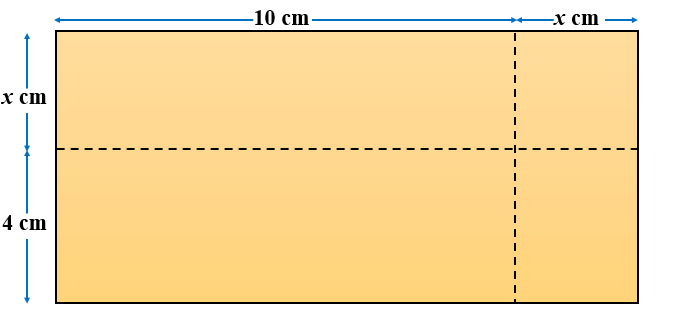
(b) Find the value of \( x \) giving your answer correct to three significant figures.
10. | GCSE Higher [134] |
A rectangular sheet of paper can be cut into two identical rectangular pieces in two different ways, either by cutting along line A or by cutting along line B.
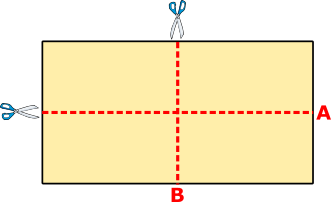
When the original sheet of paper is cut along line A, the perimeter of each of the two pieces is 56 cm.
When the original sheet of paper is cut along line B, the perimeter of each of the two pieces is 64 cm.
What is the perimeter of the original sheet of paper?
11. | GCSE Higher [129] |
Rätselzeit school has an annual sports day in which the mathematics teachers are in charge of the scoring system.
The points scored for throwing the discus are worked out using the formula:
$$p = 15(d – 4.2)$$where \(p\) is the number of points scored when the discus is thrown a distance of \(d\) metres.
(a) How many points does Homer score for throwing the discus a distance of 52 metres?
(b) How far did Marge throw the discus if she scored 492 points?
The points scored for running 400 metres are worked out using the formula:
$$p = 6(95 – t)^2$$where \(p\) is the number of points scored when the time taken is \(t\) seconds.
(c) Lisa scores 1014 points for the 400 metres race. Work out the time, in seconds, it took Lisa.
The formula for the number of points scored in the 400 metres race should not be used for \(t\gt n\).
(d) State the value of \(n\) giving a reason for your answer.
12. | GCSE Higher [321] |
Two numbers are chosen so that the sum of their squares is 25.
If those numbers are represented by \(x\) and \(y\) they will also satisfy the equation:
$$y-3x=13$$Use an algebraic method to find two possible values of \(x\) and \(y\) .
13. | GCSE Higher [178] |
The prices of two watches are in the ratio \(a:b\).
When the prices are both increased by £10, the ratio becomes \(5 : 7\).
When the prices are both reduced by £10, the ratio becomes \(1 : 3\).
Express the ratio \(a:b\) in its lowest terms.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.