

There is a great amount of satisfaction that can be obtained from solving a mathematical puzzle. There are many puzzles on this page, all with a mathematical connection, that are just waiting to be solved. You can earn Transum Trophies for the puzzles you solve.

Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.

A puzzle about the counting method that goes back and forth.
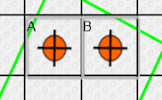
A game, a puzzle and a challenge involving counters being placed at the corners of a square on a grid.
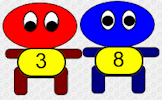
Arrange the scallywags and scoundrels on the chairs so that the numbers of any two sitting next to each other add up to a prime number.

Place the camping items into the plots on the camp site according to the clues given.

Find which numbers in a given list do not combine with other numbers on the list to make a given sum.
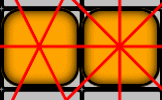
A challenge to place all nine counters on the grid in such a way that they form exactly 10 straight lines, with each line containing three counters.

Arrange the dominoes in seven squares. The number of dots along each side of the square must be equal to the number in the middle.

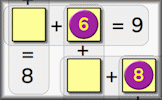
Figure out which numbers will complete the sentences in the frame correctly. A drag and drop activity.

This is an interactive version of the puzzle described by Henry Ernest Dudeney in The Canterbury Puzzles
Arrange the numbers one to nine on the stairs to obtain the given sums.

Arrange the numbers one to nine in a three by three grid to obtain the given means, medians and ranges.

Arrange the digits one to nine to make a number which is divisible in the way described.

Solve this deduction logic puzzle to find who, where and what.
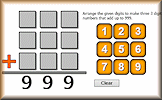
Use the digits 1 to 9 to make three 3 digit numbers which add up to 999.
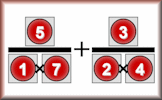
Drag the numbers one to nine onto the outlines of three fractions that combine to make one.

Arrange the numbers on the squares so that the totals along each line of three squares are equal.

An interactive activity challenging you to reproduce a pattern of coloured squares according to given clues.
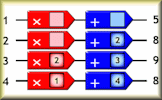
A puzzle requiring the arrangement of numbers on the function machines to link the given input numbers to the correct output.
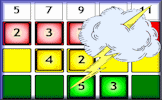
Interactive, randomly-generated, number-based logic puzzle designed to develop numeracy skills.
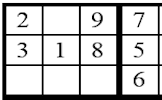
An online, interactive version of the popular number placing puzzle.
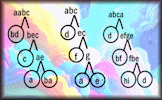
Can you determine the unique digits that will complete these factor trees?

Drag the numbers into the percentage statements to make them true.

A jumbled moving-block puzzle cube is shown as a net. Can you solve it?

Fill in the blank spaces so that the cells give the sum or the product shown in each row and column.

Partition numbers in different ways according to the clues given. The higher levels are quite hard!

Find the hidden wallaby using the clues revealed at the chosen coordinates.

The classic hourglass puzzle; Time the boiling of an egg using only the two egg timers provided.

Can you make four litres if you only have seven and five litre jugs?

Crack the code by replacing the encrypted letters in the given text. There are lots of hints provided about code breaking techniques.

Interactive jigsaw puzzles of different types of grids containing prime numbers.

An online interactive jigsaw puzzle of a grid of Thai number symbols.

An online interactive jigsaw puzzle of a grid of Chinese number symbols.
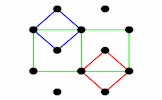
How many different sets of four dots can be joined to form a square?

Find the mathematical word from a series of guesses and clues.
Find the expression from a series of guesses and clues.

Click on six fleur-de-lis to leave an even number in each row and column.

Move the pieces of the tower from one place to another in the minimum number of moves.

Arrange the given numbers on the cross so that the sum of the numbers in both diagonals is the same.
A drag and drop activity challenging you to arrange the digits to produce the largest possible product.
Use the colours to dissect the outlines into congruent parts.

Use the colours to dissect the outlines into similar parts.
A set of ten puzzles requiring you to arrange the given digits to make an equivalent fraction.
Arrange the given numbers in a three by three grid to obtain the diagonal, row and column products.
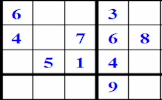
A different way to complete a Sudoku puzzle with clues available at every stage.

Arrange numbers on the plane shaped grid to produce the given totals

Fill in the squares according to the clues given by the string of numbers for each row and column.

Some picture grid puzzles which can be solved by using simultaneous equations.
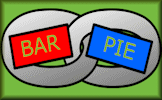
A simplified, mathematical version of the challenge seen in the British TV programme Only Connect. Find the connections between the terms.
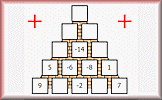
Calculate the missing numbers in these partly completed pyramid puzzles.

Numbers in the bricks are found by adding the two bricks immediately below together. Can you achieve the given target?

The chessboard has been broken into 13 pieces. Can you put it back together?
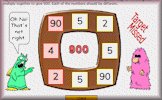
A puzzle to find four different ways of making 900 by multiplying together three different numbers.
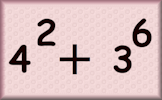
Arrange the given numbers as bases and indices in the three-term sum to make the target total.
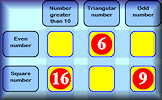
This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.

The Transum version of the traditional sliding tile puzzle.

Find where the mines are hidden without stepping on one.

Arrange the twelve pentominoes in the outline of a rectangle.
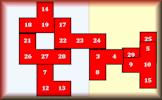
Online, interactive jigsaw puzzles of grids of numbers.
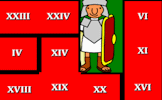
An online interactive jigsaw puzzle of a grid of Roman numerals.
Interactive jigsaw puzzles of four by four magic squares.
A number arranging puzzle with seven levels of challenge.

Can you get your car out of the very crowded car park by moving other cars forwards or backwards?
Find expressions using only one digit which equal the given targets.
Arrange the numbers from 1 to 9 to make an expression with a value of 100.

Arrange the sixteen numbers on the four by four grid so that groups of four numbers in a pattern add up to the same total.

Arrange the sixteen numbers on the octagram so that the numbers in each line add up to the same total.
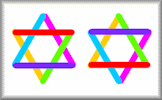
Arrange the twelve numbers on the hexagram so that the numbers in each line add up to the same total.
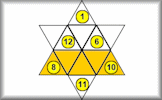
Arrange the twelve numbers in the triangles on the hexagram so that the numbers in each line of five triangles add up to the same total.

Arrange the given digits to make six 3-digit numbers that combine in an awesome way.

Arrange the numbered footballs on the goal posts to make three, 3-number products that are all the same.
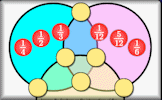
Quite a challenging number placing puzzle involving fractions.

Each row, column and diagonal should produce the same sum.
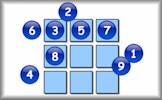
Like the magic square but all of the totals should be different.
Solve the problem of getting four people through a tunnel with one torch in the minimum amount of time.

Can you find a 6 digit number containing two each of the digits one to three which obeys the rules given?
Can you draw these diagrams without lifting your pencil from the paper? This is an interactive version of the traditional puzzle.

The traditional River Crossing challenge. Can you do it in the smallest number of moves?
Arrange the numbers from 1 to 6 in the spaces to make the division calculation correct.

Arrange a rota for the Scouts to travel in boats so that they are with different people each day.
Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
Arrange the given number tiles to make two 2 digit numbers that add up to the given total.
A great puzzle requiring you to use all of the cards to create a continuous red line from start to finish.
Change the numbers on the apples so that the number on the lemon is the given total.
Make a schedule for the 24-hour Darts Marathon which will take into account everyone's requests and keep everyone happy.
Let the psychic read the cards and magically reveal the number you have secretly chosen. What is the mathematics that makes this trick work?

Interactive, randomly-generated, number-based logic puzzle designed to develop numeracy skills.
Arrange the numbers from 1 to 14 in the spaces to make the sums correct. How fast can you do it?

Interactive number-based logic puzzles similar to those featuring in daily newspapers.

Arrange the given digits to make a Latin square with the given row and column calculation results.
Arrange the nine pieces of the puzzle on the grid to make different polygons.
A fewest-moves, counter-swapping challenge invented in northern Thailand.
A logic challenge requiring a strategy to update each of the numbers in a grid.

Drag the numbers into the red cells so that the sum of the three numbers in each row and each column is a prime number.
Arrange the cards to create a valid mathematical statement.

Toss the pancakes until they are neatly stacked in order of size. Find how to do this using the smallest number of moves.

Find the mathematical words in the grid of letters.
Help the cops catch the robbers by finding the vectors that will end the chase.
Solve the number puzzles drawn on the pavement of Trafalgar Square in London.
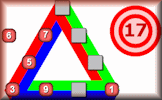
Arrange the digits 1 to 9 on the triangle so that the sum of the numbers along each side is equal to the given total.

Arrange the given digits to make three numbers such that the third is the product of the first and the second.

Arrange the digits to make three 3 digit numbers such that the second is double the first and the third is three times the first.
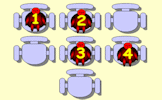
The students numbered 1 to 8 should sit on the chairs so that no two consecutively numbered students sit next to each other.
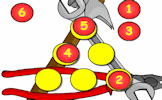
In how many different ways can the numbers be arranged to give the same totals?
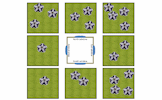
Drag the 20 flowers into the gardens so that 9 flowers are visible from each window of the house.

Join up the stars to find the hidden regular polygons.
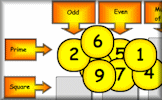
Place the nine numbers in the table so they obey the row and column headings about the properties of the numbers.

Use the pieces of the T puzzle to fit into the outlines provided. A drag, rotate and drop interactive challenge.
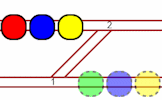
Move the trams to their indicated parking places in the shunting yard as quickly as possible.
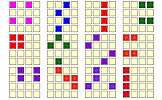
Find all of the possible ways of making the magic total from the numbers in this four by four magic square.
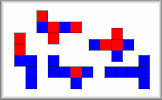
Find all the ways of painting the faces of cubes using only two colours.

Arrange the given digits to make three numbers such that two of them add up to the third.

Use the pieces of the tangram puzzle to make the basic shapes then complete the table showing which shapes are possible.
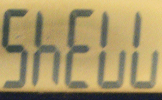
Turn your calculator upside down to make words out of the answers to these questions.

Vowels have been taken out of mathematical words. Can you recognise them?
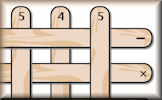
If you were to pick up the sticks from this pile so that you were always removing the top stick what calculation would you create?
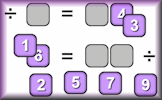
Arrange the digits one to nine on the spaces provided to make two division calculations containing multiples of three.
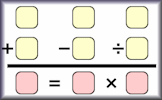
Arrange the digits one to nine to make the four calculations correct.

Place the digits one to nine in each of the regions created by the Olympic rings so that the sum of the numbers in each ring is the same.
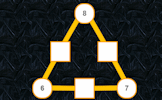
Find the missing numbers in these triangular, self-checking puzzles and discover the wonders of these fascinating structures.

Divide the grid into rectangular pieces so that the area of each piece is the same as the number it contains.

A hands on activity requiring students to arrange Christmas ornaments in a square box.
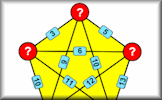
Find the five numbers which when added or multiplied together in pairs to produce the given sums or products.
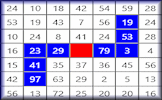
Find the path to the centre of the labyrinth by moving along the prime numbers.
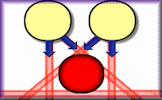
Can you arrange the seven counters on the grid despite their truculent behaviour?
An interactive mathematical crossword for you to do online. Find the missing words from the given clues.
Speakers with Blue Teeth
If pounds change places with pence can you calculate the cost of a speaker?
The Price of Easter Eggs
The cost of Easter eggs came down by 30p per dozen. How many did I buy?
Sharing Trophies
How can Miss Adgood share her trophies between her three younger brothers?
Triangles in Hexagons
How many different asymmetrical triangles can be drawn by joining three of the vertices of a regular hexagon?
Teaching the Wrong Class
Will the last teacher out of the staffroom teach their timetabled class?
Prancer's Walk
How far did Prancer walk while Santa was delivering presents to Tran Towers?
Planets Orbiting Vesperion
How many moons does Nymeria have given some mean clues?
Pumpkin Price Puzzle
What was the mean number of pumpkins that could be bought for £20?
Winter Draws On
What fraction of the group wore all three items: hats, scarves, and gloves?
Three Numbers, Four Clues
Given information about the mean, median and range, figure out what the three numbers are.
Pirate Pearl's Treasure
Can you figure out how many stones of each colour there are in the pirate's cove?
Twice the Wig
A judge is twice as old as her wig was when she was as old as her wig is now.
Maths Equipment
What percentage of the class brought all the required maths equipment to the lesson?
What is the letter D worth?
From the clues about A, B and C can you work out the value of D?
Easter Egg Evaluation
What is the largest number of eggs that cannot be purchased using a combination of the given basket sizes?
Leap Year February
What birthday did Attika celebrate in the last leap year of the last century?
Justin's New Year's Resolution
How many days in January will Justin be able to go for a jog?
Mean Spending On Christmas Presents
Work out the cost of the most expensive gift given the mean cost and other clues.
End of Squares and Cubes
How many positive two-digit numbers are there whose square and cube both end in the same digit?
Whopping Million
Find two whole numbers, not containing zeros, that when multiplied, give a million.
Divided Dartboard
A dartboard splits in two. One piece's numbers sum to twice the other's. Where's the break?
Calamity Cousins
Work out the range of the ages of the cousins given the average clues.
Sum-What?
If x and y are positive integers and x + xy + y = 90, what is the sum of x and y?
Indices are powerful exponents!
If x squared equals sixteen to the power of x. Find the value of x.
Letters in a Sentence
Write a number in words in the gap in the sentence that will make the statement true.
Cupcakes and Easter Eggs
Work out how many children there were eating cupcakes from the given clues.
Palindromic Numbers
Work out Mr Wheeler's average speed given the palindromic numbers seen on his odometer.
Six Three-Letter Words
Work out the teacher's favourite word from the statements made by the clever students.
Coloured Ornaments
How many ornaments are on the tree and how many of each colour are there?
Same Probability
Why are the probabilities the same of picking two balls with an odd sum from two different pots?
Viral Maths
What is the correct result of the calculation that has become a viral talking point on the internet?
Holiday Island Weather
Work out the length of my holiday from the clues about the weather.
Weighted Puzzle
What four weights would enable me to use the balance scales to weigh any object from 1 to 40 pounds?
Alphabetical Numbers
Arange all the natural numbers in alphabetical order - which number comes second?
Strange Dice
Number the faces of the cubes to make strange dice with a minimum face sum.
Leaving Transumvania
Find where the drone catches up with the ship given their relative speeds.
Rolling Dice
Find a nice method to work out which number on the dice is uppermost after rolling across a chess board.
Sisters Outnumbering Brothers
Work out the total number of children in Rachel's family using the clues about brothers and sisters.
Time and Calendars
How many times in a 24 hour period do all four digits on my bedside clock change at the same time?
Santa's Small Window
How do you increase the area of a window without changing its height or width?
How Much Richer?
A puzzle about the relative wealth of Maureen compared to Doreen.
Factor Shopping
Find the prices of the items bought if they are different and all factors of the total bill.
Splitting Ten for a Product
Which of the many ways of splitting ten gives the largest product?
A Frobenius coin problem
What is the largest amount that cannot be made with 5p and 7p coins?
Bus Fare Premonition
How did the bus driver know how much to charge Mrs P and Mrs Q?
A Half Mean Angle
Find the size of the angle at A if it is half of the mean of the angles at B and C.
Chris and his Unpredictable Kids
A think of a number puzzle with an unpredictable element.
Two-Faced and Blue
How many of the smaller cubes that make up the 3x3 cube have two faces painted blue?
Santa is Cool
What temperature is reported using the same number in Celsius and Fahrenheit?
Three Trios of Triplets Thrice
A simple question that seventy two percent of a group of people got wrong.
Six Ropes
Can the pirates win their freedom by tying the six pieces of rope into one large loop?
Bogdan and Wally
In what order should you play Ultimate Noughts and Crosses against Wally and Bogdan?
Eva's Eggs and Fickle Fractions
How many eggs did Eva take to market in order to make those strange half sales?
Feeding Fools and Horses
How long will the horse feed last the horses after some of them left the stables?
Balancing Balloons
How many balloons must Jamie give to Ben to balance the balloon equation?
A Puzzle from Carl
Carl's puzzle is about the result of dividing the product of his parents' ages by double his own age.
Odds from evens up to 2020
Subract the sum of the odd numbers less than 2020 from the sum of the even numbers less than 2020.
Noel in Lapland
Work out the length of Noel's trip to Lapland given the details of the weather conditions.
Multiple Remainders
What is the second smallest number such that when it is divided by 5 the remainder is 4, and when divided by 7 the remainder is 6?
Coaches to Cambridge
Can you figure out which coach I travelled in when I went to Cambridge?
Percy Cod's Kids
Percy Cod was talking about his children. Can you work out their ages given the ratios?
Carrot-eating Critters
Work out how many of each kind of animal are in the field from their carrot-eating habits.
Patsy Loves Percy
The strange case of Percy who seems to be getting older very quickly
Monkeys, Kittens and Dogs
Who is most likely to be able to work out the square root of 121?
Feed The Horses
How long will the remaining feed last the horses that have not been sold?
Strange Addition
If I start at five and add six I get eleven but if I start at six and add seven I get one.
Prime Permutations
Of all the permutations of 1 to 9 used to make nine-digit numbers, how many are prime?
4-Digit Hotel Room Safe Code
Can you work out what number I used to lock and unlock my hotel room safe?
Choir Eye Colour
Figure out the percentage of choir members that do not have blue eyes from the clues given.
Calculator Keys at the Corners of a Rectangle
A question about the four keys at the corners of a rectangle on a calculator.
Average House Numbers
Work out the house numbers from the clues about the mean, median and mode.
Five integers with a product of 12
Can you find five integers that multiply together to give twelve?
Square in a Rectangle
What is the largest square that can be drawn in the corner of a 10cm by 15cm rectangle?
London Marathon
A question about the average speed required for the second half of the marathon.
Cutting the Lawn
Aynuk and Ayli cut half of the lawn each. How long is each side of the square lawn?
Forty Five in Four Parts
Split the number 45 into four parts according to the given information.
Shrivelled Spuds
Work out the weight of the potatoes after they have been left out in the sun to dry.
Transposition Error
Work out the bank balance given information about the transposition error.
Counting Sheep
Work out the number of sheep owned by Percy and Patsy from the given clues.
Juggling with Egg Timers
Can you time exactly nine minutes using the four and seven minute egg timers?
Permutation Sum
What is sum of all the four digit numbers containing all of the digits one to four?
Odd Probability
What is the probability that two random numbers are both even if they are not both odd?
Regions in Circles
Calculate the number of regions in a circle formed by intersecting chords.
Brothers and Sisters
Can you work out the number of children in the Numlove family given the clues about brothers and sisters?
Exam Average
What mark is required in the last exam to achieve an 80% overall average?
Holy Sphere
Calculate the remaining volume of the sphere after a cylindrical hole has been drilled through the centre
Jumping Flea
How many different places could the flea find itself after 8 foot-long jumps either north, south, east or west?
Last Digit
How many positive two-digit numbers are there whose square and cube both end in the same digit?
Central Station
The probability that the next train to leave will be going north is five times the probability that the next train to leave will be going south.
Separated Twins
Work out the combination of the safe given the clues about pairs of numbers.
Divisible By Three
A puzzle about two digit numbers that can be made from ten different digits.
Letters In Numbers
A brand new puzzle involving the letters in numbers when written as words.
Square Angled Triangle
The angles of a triangle are all square numbers. What are they?
Tri-Junction Puzzle
What is the probability of the three cars arriving at the road junction not being involved in an accident?
Two Prime Squares
What is the smallest square number (greater than one) that cannot be expressed as the sum of two prime numbers?
The Missing Pound
Where did the missing pound go in this story about three people visiting a restaurant?
Ticks, Tocks, Tacks and Tucks
Find how ticks compare to tocks, tacks and tucks from the given information.
The Power of Christmas
A question about indices to get you thinking mathematically at this festive time of year.
Ant and Dec
What single question could Dec ask Ant to find out what he is thinking?
Three Mathematicians
How can the third mathematician be so certain that everyone wants a drink?
Unfinished Game
If the coin tossing game was cut short how would you share the winnings?
Best Dice
Which of the unusual dice would you choose to give you the best chance of winning the prize?
The Birthday Problem
What is the probability of two or more pupils in a class having the same birthday?
Twelve Days of Christmas
Can you figure out exactly how many gifts the true love sends during the twelve days of the Christmas holiday?
Chased by a Bear
A puzzle about an explorer being chased by a bear along with a question about imperial and metric measures with Measurement Man
Halloween Bases
A puzzle about Why is halloween like Christmas along with news of the new Number Skills Inventory
Torch Tunnel
A puzzle about four people making their way through a tunnel with just one torch along with news of the new numerology page
Cube in Milk
A puzzle about a cube being lowered into a bucket of milk along with news of the new shunting puzzles
Alphanumbetical
A challenge to find the number which when written as a word has all the letters in alphabetical order.

Arithmagons
This lesson starter requires pupils to find the missing numbers in this partly completed arithmagon puzzle.

Christmas Ornaments
A Maths Starter activity requiring students to arrange Christmas ornaments in a square box.

ClockEquate
Can you use the digits on the left of this clock along with any mathematical operations to equal the digits on the right?

Coins On The Table
A puzzle about the number of coins on a table given information about fractions of them.

Eleven Plus Two
Rearrange the letters in the ex

House Numbers
The numbers on five houses next to each other add up to 70. What are those five numbers?

How Many Squares? 1
Work out how many squares are there altogether in the given pattern then tackle the chess board.

Loopy Lake
Match the fractions to their decimal equivalents and join them with lines that do not cross.

Maths In School
Find mathematical words which can be made by using the letters in the name of your school?

Mirror Maths
The bottom half of some symmetrical calculations are shown above. Can you work out the answers?

Missing Square Puzzle
The missing square puzzle is an optical illusion used to help students reason about geometrical figures.

One Digit 100
How many ways can you write an expression for 100 which only uses the same digit repeated and any operations?

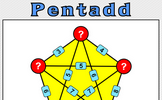
Pentadd
Five numbers are added together in pairs and the sums shown. What might the five numbers be?
Pipeline Puzzle
Arrange the numbers so that the totals of the three numbers along any pipe are the same.

Roundabout
Go around the roundabout performing each of the operations. Which starting point gives the largest answer?

Route to Las Vegas
Work out the cheapest way from Los Angeles to Las Vegas by choosing the best route and adding up the given numbers.

Rows of Roses
Can you draw 4 straight lines, without taking your pencil off the paper, which pass through all 9 roses?

Secret Symbol
Place a symbol between the four and the five to get a number greater than four and less than five.

Separated Twins
Can you find a 14 digit number containing two each of the digits one to seven which obeys the rules given?

Small Satisfaction
Arrange the digits one to nine in the grid so that they obey the row and column headings.

Suko
Interactive number-based logic puzzle similar to those featuring in The Times and Telegraph newspapers.

Sum of the Signs
Each traffic sign stands for a number. Some of the sums of rows and columns are shown. What numbers might the signs stand for?

THOAN
THOAN stands for 'Think of a number' and there are four randomly generated THOAN puzzles to solve.

Tool Triangle
Place the numbers on the triangle so that the totals along each of the sides are equal.

Angle Thinking
Find the range of possible angles, x, for which tan x > cos x > sin x
Average Cycling Speed
Work out the average speed of two journeys. The obvious answer is not the correct answer.
Bertrand's Box Paradox
Bertrand's box paradox is a paradox of elementary probability theory, first posed by Joseph Bertrand in 1889
Best Dice
Which of the unusual dice would you choose to give you the best chance of winning the prize?
Blue Sky Rectangle
Find the area of the rectangle given information about the two connected right-angles triangles.
Charging Rhinos
Find the easy way to solve this kinematics problem involving a fly and two rhinos.
Cheryl's Birthday
Use a process of elimination to work out the correct date from the clues given.
Divisible by 11
Can you prove that a three digit number whose first and third digits add up to the value of the second digit must be divisible by eleven?
Double or Half?
At ten percent change per day is doubling achieved faster than halving?
Exponential Trigonometry
Find, in degrees, all eight of the solutions to the given exponential, trigonometric equation
Fence Optimisation
Find the length of a rectangle enclosing the largest possible area.
Find The Radius
Find the radius of the circle from the small amount of information provided.
Four Fraction Division
Explain why the answer to a series of fraction divisions is a whole number.
Geometry Snack
Find the value of the marked angle in this diagram from the book Geometry Snacks
Grandmother
How far would grandma have travelled after a suitably large number of days given her walking regime?
Hands Together
The hands of a clock are together at midnight. At what time are they next together?
How Many Left Handers?
Work out the number of members if the probability of left-handed members being randomly selected is given.
Hundred and Fifty Percent
Divide 110 into two parts so that the larger part is 150% of the smaller part.
Key Eleven
Prove that a four digit number constructed in a certain way will be a multiple of eleven.
Log Perfection
Determine whether the given statements containing logarithms are true or false
Maximum Product
Two numbers add up to 10. What's the largest possible product they could have?
Nine Digit Numbers
How many different nine digit numbers are their that contain each of the digits from one to nine?
One Torch Tunnel
What is the least amount of time for all four people to walk through the tunnel?
Paper Ratio
Calculate the ratio of the sides of an A4 sheet of paper without any measuring.
Paper Surprising Perimeter
Find the perimeter of a folded sheet of A4 paper as described in this short video.
Parallel Graphs
Determine from their equations which of the straight line graphs are parallel and perpendicular.
Penny Bags
Can you place 63 pennies in bags in such a way that you can give away any amount of money (from 1p to 63p) by giving a selection of these prepacked bags?
Permutable Functions
Find pairs of functions that are commutative under composition.
Piece of String
Find where a piece of string should be cut to form a circle and a square of equal areas.
Pizza Slice
A problem which can be solved by considering the areas of a triangle and a sector of a circle.
Powers from the Past
Find the value of x from the equation on the classroom chalk board
Product of Indices
Find the product of the unknown indices that feature in two equations
Quad Midpoints
What shape is created when the midpoints of the sides of a quadrilateral are joined together?
Restrained Flea
How many different places could the flea find itself after 8 foot-long jumps either north, south, east or west?
Reverse Connection
Find a general rule for the difference between a two digit number and that same number with the digits reversed.
Rice on a Chess Board
How many grains of rice are on a chess board if each square has twice the number of grains as the previous square.
Road Connections
Design roads to connect four houses that are on the corners of a square, side of length one mile, to minimise the total length of the roads.
Rope Around The World
Imagine a long rope wrapped around Earth's equator - One metre longer than it needs to be.
Same Series Sum
Find an arithmetic series and a geometric series that have the same sum of the first five terms.
Same Three Digits
Find ex
Seventeen Camels
Explain the mathematics of the classic ninteenth century fraction sharing story.
Singers and Dancers
What fraction of the singers and dancers are both singers and dancers?
Single Fraction
Simplify an expression involving fractions, exponents and a square root.
Sorcerer's Apprentices
The difference between random selection and an 'at least' scenario involving sorcerer's apprentices.
Sphere Hole
Find the volume of the remaining part of a sphere after a 10cm cylindrical hole has been drilled through it.
Square in Rectangle
Find the area of a square drawn under the diagonal of a rectangle
Test Scores
Explore the misconception that when adding fractions you add both the numerators and the denominators
Three Right Triangles
Calculate the lengths of the unlabelled sides of these right-angled triangles.
Transum Tonic
What is the largest number of bottles that it is not possible to buy if they come in packs of 6, 9, and 20?
Tri-Junction
A real life situation that can be analysed with the use of a tree diagram.
Two Pots
Use tree diagrams to find the surprising result that probabilities of different situations are the same.
Two real numbers
The sum of the reciprocals of two real numbers is -1, and the sum of their cubes is 4. What are they?
Unfinished Game
Share the prize in a fair ratio according to the probability of each player winning.
Uniqueness Starter
Find answers to questions that no one else in the class has thought of.
Unlucky Seven Eleven
Follow the instructions to multiply a chosen number then explain the result you get.
Victorian Times Comparison
Is 10! larger or smaller than the number of seconds in six weeks?
Vowel Code
How many ways can you create a code for the vowels by assigning to each vowel a different vowel?
What Question?
Write down all the possible questions that could have been asked if this was the Venn diagram provided in a mathematics exam.
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Eric Levy, United States
Thursday, November 17, 2016
"Thank you for the podcasts! I really enjoy the puzzles. This relates to the 5/29/15 podcast re: coin flipping game that was stopped before completion. The flips when stopped were two Heads and one Tail. You indicate that the options on next 2 tosses are HH, TH, HT, and TT. Since the game stops when one person reaches 3 points, wouldn't HH and HT be the same, as the second flip isn't needed? This seems to match your ultimate answer of 75% and 25%, though ... with the person with Tails only winning with TT, which is 25% chance. I get the same answer but intermediate steps differ. Am I looking at this incorrectly? Thanks!."
Transum,
Thursday, November 17, 2016
"Dear Eric, Thanks so much for your observations and you are completely right. The only reason I chose to list the next two outcomes was to produce equally likely outcomes making the arithmetic very slightly easier. I am glad you enjoy the puzzles."
Dubai English Speaking School,
Wednesday, January 24, 2018
"Six Yellow are working together using Transum Maths this morning...head to head on puzzles ranging from Darts to Factors Connect 4
 "
"
Elena Bezoari, Twitter
Saturday, June 8, 2019
Ann, London
Tuesday, September 3, 2019
"Hi there!
Great maths puzzles & activities. Thank you.
Do you have the answers?
[Transum: Hello Ann, Thanks for leaving a comment on the Transum Puzzles page. Yes, each of the puzzles has an answer that appears when you are logged in as a subscriber. You can find a subscription application form here. "
Mike Park, United States
Saturday, October 2, 2021
"I must commend you on nurturing such a thorough and ingenious website of math problems. You offer great exercises, puzzles, review material, and so much more. I really enjoyed using Transum Math."
Whitney Edmondson, Linkedin
Wednesday, March 29, 2023
"This month we ran our puzzle and problem solving team competition amongst the different grades. We decided to improve from the traditional "hard maths" questions and have inquiry and thinking stations. This wasn't about who was the best at just Maths, it was about who was the best at doing Maths using all the MYP ATL Skills.
Thanks again to the fantastic Transum.org site for the puzzles I used to create the stations. To mention a few brilliant aspects about using this site for Maths stations.
On refreshing you get a new but similar puzzle, points are often generated, instructions included for staff to read and creative interactive levels you can adjust depending on the grade...Completely FREE!"