|
|
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
Jack knows that he needs 4 litres of paint to cover a rectangular wall that is 3m by 8m.
Paint is sold in 3 litre tins.
Jack wants to paint a rectangular wall that is 4m by 20m.
He has 5 tins of paint.
(a) Has Jack got enough paint to cover the wall that is 4m by 20m? You must show all your working.
Jack opens the 5 tins of paint. He finds that 4 of the tins contain 3 litres of paint. The other tin contains 1.5 litres of paint.
(b) Does this affect whether Jack has enough paint to cover his wall? Give a reason for your answer.
2. | GCSE Higher |
The circumference of the red circle is 80% of the circumference of the blue circle.
(a) Find the ratio of the area of the red circle to the area of the blue circle.
The green square has sides of length \(a\) cm.
The yellow square has sides of length \(b\) cm.
The area of the green square is 21% greater than the area of the yellow square.
(b) Work out the ratio \(a : b\)
3. | GCSE Higher |
The three boxes pictured below are mathematically similar.
The edges of the largest box are twice as long as the edges of the smallest box.
The volume of the middle box is twice as big as the volume of the smallest box.
What fraction is the volume of the middle box of the volume of the largest box?
4. | GCSE Higher |
Two similar pentagonal based pyramids have surface areas 200 cm2 and 50 cm2 respectively.
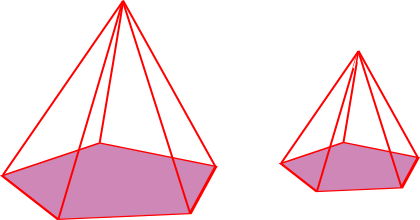
The volume of the larger pyramid is 800 cm3.
Show that the volume of the smaller pyramid is 100 cm3.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
