
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | IB Studies [82] |
A function is given as \(f(x)=3x^2-6x+4+\frac3x,-2\le x \le 4, x\ne 0\).
(a) Find the derivative of the function. (b) Find the coordinates of the local minimum point of \(f(x)\) in the given domain using your calculator.2. | IB Studies [83] |
Consider the graph of the function \(f(x)=7-3x^2-x^3\)
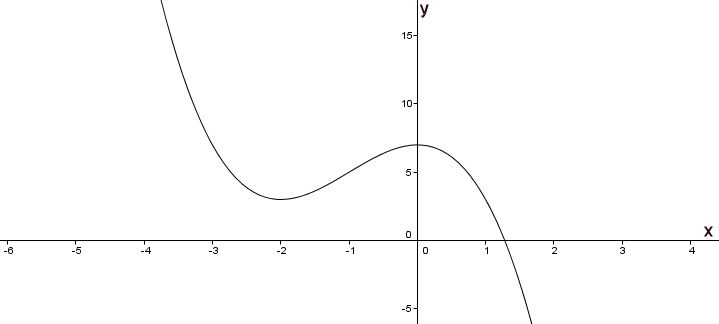
(a) Label the local maximum as A on the graph.
(b) Label the local minimum as B on the graph.
(c) Write down the interval where \(f(x)>5\).
(d) Draw the tangent to the curve at \(x=-3\) on the graph.
(e) Write down the equation of the tangent at \(x=-3\).
3. | IB Studies [104] |
A child's play tent is made in the shape of half a cylinder. It is constructed from a fibreglass frame with material pulled tightly around it. The fibreglass frame consists of a rectangular base, two semi-circular ends and two further support rods, as shown in the following diagram.
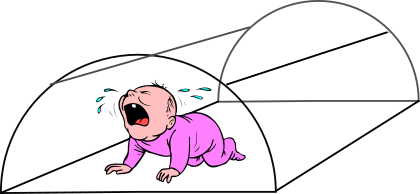
The semicircular ends each have radius \(r\) and the support rods each have length \(d\).
Let F be the total length of fibreglass used in the frame of the play tent.
(a) Write down an ex
The volume of the play tent is 0.95 m3.
(b) Write down an equation for the volume of the play tent in terms of \(r\), \(d\) and \(\pi\).
(c) Show that \(F = 2\pi r + 4r + \frac{7.6}{\pi r^2}\)
(d) Find \(\frac{dF}{dr}\)
The play tent is designed so that the length of fibreglass used in its frame is a minimum.
(e) Find the value of \(r\) for which \(F\) is a minimum.
(f) Calculate the value of \(d\) for which \(F\) is a minimum.
(g) Calculate the minimum value of \(F\).
4. | IB Studies [110] |
A package is in the shape of a cuboid and has a length \(l\) cm, width \(w\) cm and height of 12 cm.
(a) Express the volume of the package in terms of \(l\) and \(w\).
The total volume of the package is 2400 cm3.
(b) Show that \(l=\frac{200}{w}\).
The package is tied up using a length of red string that fits exactly around the package in two different directions, as shown in the following diagram (not to scale).
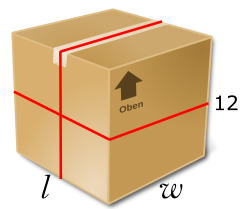
(c) Show that the length of string, \(x\)cm, required to tie up the package can be written as \(24+4w+\frac{400}{w}\)
(d) Sketch the graph of \(x\) for \(0\lt w \le 12\), clearly showing the local minimum point.
(e) Find \(\frac{dx}{dw}\).
(f) Find the value of \(w\) for which \(x\) is a minimum.
(g) Find the value, \(l\), of the package for which the length of string is a minimum.
(h) Find the minimum length of string required to tie up the package.
5. | IB Analysis and Approaches [567] |
A particle moves in a straight line. During the first nine seconds the velocity, \(v\) ms-1 of the particle at time \(t\) seconds is given by:
$$ v(t) = t \cos(t+5) $$
The following diagram shows the graph of v:
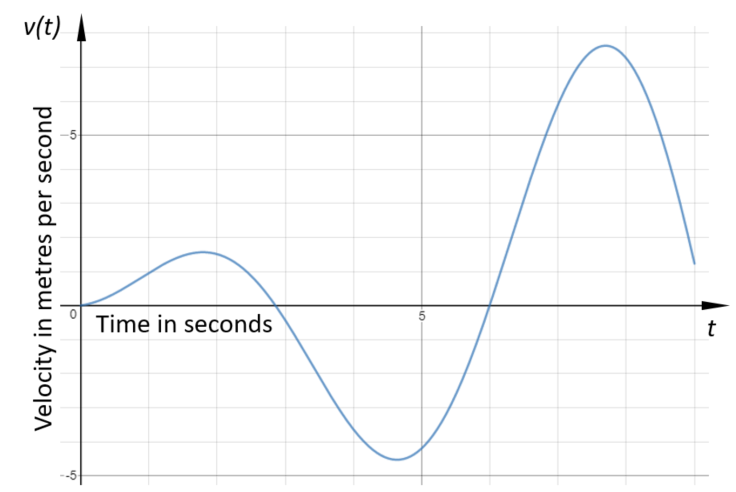
(a) Find the maximum value of \(v\).
(b) Find the acceleration of the particle when t = 6.
(c) Find the total distance travelled by the particle.
6. | IB Studies [27] |
Consider the function \(f(x)=6 - ax+\frac 3{x^2},x\neq 0\)
(a) Write down the equation of the vertical asymptote of the graph of \(y=f(x)\).
(b) Write down \(f'(x)\)
The line T is the tangent to the graph of \(y=f(x)\) at the point where \(x=1\) and it has a gradient of -8.
(c) Show that \(a=2\).
(d) Find the equation of T.
(e) Using your calculator find the coordinates of the point where the graph of \(y=f(x)\) intersects the x-axis.
(f) The line T also intersects \(f(x)\) when \(-2\le x\le 0\). Find the coordinates of this intersection.
7. | IB Analysis and Approaches [594] |
The function \(f\) is defined for all \(x \in \mathbb{R}\). The line with equation \(y=5x+3\) is the tangent to the graph of \(f\) at \(x = 2\)
(a) Write down the value of \(f'(2)\).
(b) Find \(f(2)\).
The function \(g\) is defined for all \(x \in \mathbb{R}\) where \(g(x) = x^3 - 3x\) and \(h(x) = f(g(x)) \).
(c) Find \(h(2)\).
(d) Hence find the equation of the tangent to the graph of \(h\) at \(x = 2\).
8. | IB Analysis and Approaches [417] |
Consider the cubic function \(f(x)=\frac{1}{6}x^3-2x^2+6x-2\)
(a) Find \(f'(x)\)
The graph of \(f\) has horizontal tangents at the points where \(x = a\) and \(x = b\) where \( a < b \).
(b) Find the value of \(a\) and the value of \(b\)
(c) Sketch the graph of \(y = f'(x)\).
(d) Hence explain why the graph of \(f\) has a local maximum point at \(x = a\).
(e) Find \(f''(b) \).
(f) Hence, use your answer to part (e) to show that the graph of \(f\) has a local minimum point at \(x = b\).
(g) Find the coordinates of the point where the normal to the graph of \(f\) at \(x = a\) and the tangent to the graph of \(f\) at \(x = b\) intersect.
9. | IB Studies [22] |
Consider the function \(f(x)=x^3-9x+2\).
(a) Sketch the graph of \(y=f(x)\) for \(-4\le x\le 4\) and \(-14\le y\le 14\) showing clearly the axes intercepts and local maximum and minimum points. Use a scale of 2 cm to represent 1 unit on the x-axis, and a scale of 1 cm to represent 2 units on the y-axis.
(b) Find the value of \(f(-1)\).
(c) Write down the coordinates of the y-intercept of the graph of \(f(x)\).
(d) Find \(f'(x)\).
(e) Find \(f'(-1)\)
(f) Explain what \(f'(-1)\) represents.
(g) Find the equation of the tangent to the graph of \(f(x)\) at the point where x is –1.
R and S are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of R is \(a\) , and the x-coordinate of S is \(b\) , \(b \gt a\).
(h) Write down the value of \(a\) ;
(i) Write down the value of \(b\).
(j) Describe the behaviour of \(f(x)\) for \(a \lt x \lt b\).
10. | IB Standard [57] |
Let \(f(x)=\frac{g(x)}{h(x)}\), where \(g(3)=36\), \(h(3)=12\), \(g'(3)=10\) and \(h'(3)=4\). Find the equation of the normal to the graph of \(f\) at \(x=3\).
11. | IB Analysis and Approaches [385] |
The displacement, in millimetres, of a particle from an origin, O, at time t seconds, is given by \(s(t) = t^3 cos t + 5t sin t\) where \( 0 \le t \le 5 \) .
(a) Find the maximum distance of the particle from O.
(b) Find the acceleration of the particle at the instant it first changes direction.
12. | IB Analysis and Approaches [657] |
A circle with equation \(x^2+y^2=25 \) has centre \((0,0)\) and radius 5.
A trapezium, ABCD, is inscribed in the circle with its vertices at \( A(x,y), B(4,-3), C(-4,-3) \text{ and } D(-x,y)\), where A and D are variable points in the first and second quadrants respectively. This is shown in the following sketch.
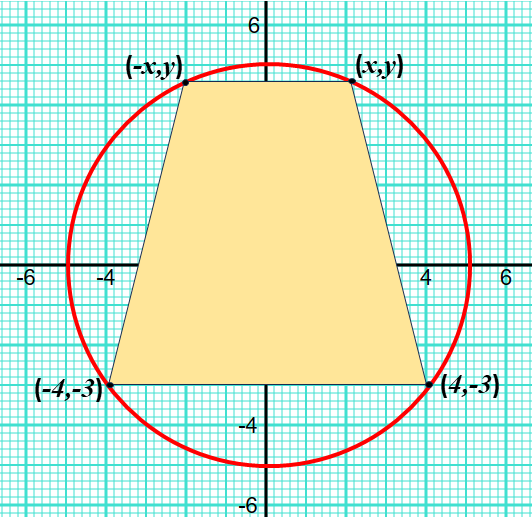
(a) For point A, show that \(y = \sqrt{25-x^2} \).
(b) Hence, find an expression for T, the area of trapezium ABCD, in terms of x.
(c) Show that \( \dfrac{dT}{dx} = 3 - \dfrac{2x^2 +4x -25}{\sqrt{25-x^2}} \).
(d) Hence or otherwise, find the value of \(x\) such that T is a maximum.
13. | IB Standard [36] |
The function \(f\) is defined as follows:
$$f(x)=\frac{122}{1+60e^{-0.3x}}$$(a) Calculate \(f(0)\).
(b) Find a value of \(x\) for which \(f(x)=85\)
(c) Find the range of \(f\).
(d) Show that:
$$f'(x)=\frac{2196e^{-0.3x}}{(1+60e^{-0.3x})^2}$$(e) Find the maximum rate of change of \(f\).
14. | IB Analysis and Approaches [556] |
Consider the functions
$$f(x) = m-x^2 - 2xn - n^2$$ $$g(x) = \frac{e^x}{e^2} + \frac{m}{2}$$where \(m, n \in \mathbb R\)
(a) Find \( f'(x)\).
(b) Find \( g'(x)\).
The graphs of \(f\) and \(g\) have a common, non-vertical tangent at \(x=3\).
(c) Find expressions for \(m\) and \(n\) in terms of \(e\).
15. | IB Standard [66] |
The following diagram shows part of the graph of \(y=f (x)\)
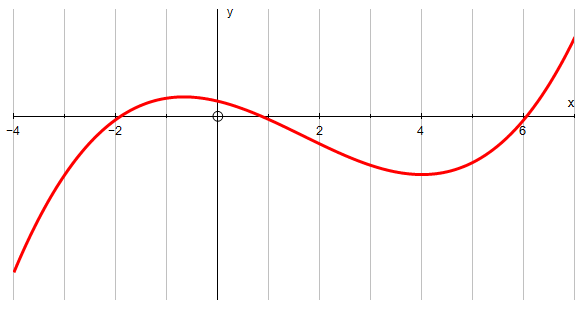
The graph has a local maximum where \(x=- \frac23\), and a local minimum where \(x=4\).
sketch the graph of \(y=f'(x)\) for \(-4\le x \le 7\)
Write down the following in order from least to greatest: \(f(2),f'(4)\) and \(f''(4)\).
16. | A-Level [452] |
Moresum Soup is sold in cans with a capacities of 400ml each. Each can is in the shape of a right circular cylinder with radius \(r\) cm and height \(h\) cm.
(a) Assuming that the can is made from a metal of negligible thickness prove that the total surface area, A cm2, of the can is given by the following formula:
$$ A= 2 \pi r^2 + \frac{800}{r} $$(b) Given that r can vary, find the dimensions of a can that has minimum surface area.
17. | IB Standard [32] |
Make a sketch of a graph showing the velocity (in \(ms^{-1}\)) against time of a particle travelling for six seconds according to the equation:
$$v=e^{\sin t}-1$$(a) Find the point at which the graph crosses the \(t\) axis.
(b) How far does the particle travel during these first six seconds?
18. | IB Analysis and Approaches [561] |
The function \(f\) is such that \(f(x) = \frac{\ln2x}{x^3} \) where \(x \gt 0\).
(a) Find the first derivative of the function, \( f'(x) \).
(b) The graph of \( y=f(x) \) has a horizontal tangent at the point T. Find the coordinates of T.
(c) Show that T is a local maximum point by considering the second derivative, \( f''(x) \).
(d) Find the values of \(x\) for which \( f(x) \gt 0 \).
(e) Sketch the graph of \( f \) showing clearly the value of the x-intercept and the approximate position of point T.
19. | IB Analysis and Approaches [569] |
Consider the function \(f\) defined by \(f(x) = 25e^{x-5}\) for \(x \in \mathbb{R}^+\).
(a) Find the coordinates of the points where the graph of \(f\) intersects the line \(y=x\).
The line \(L\) has a gradient of \(-1\) and is a normal to the graph of \(f\) at the point \(R\).
(b) Find the exact coordinates of \(R\).
(c) Show that the equation of the line \(L\) is \(y=-x+6- \ln{25}\).
(d) Find the area of the region enclosed by the graph of \(f\) and its inverse.
20. | IB Analysis and Approaches [602] |
The following diagram shows the graph of \(f'\), the first derivative of a function \(f\).
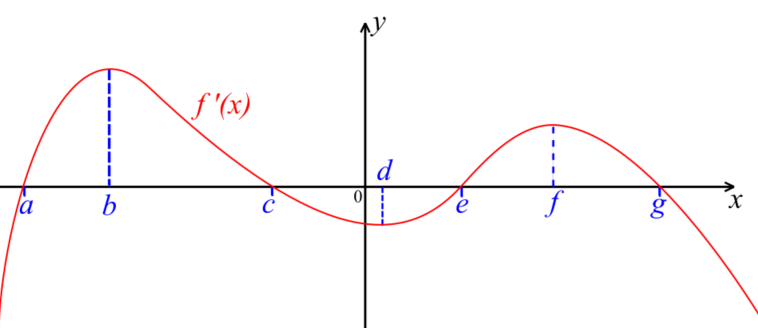
The graph of \(f'\) has x-intercepts at \(x=a, x=c, x=e \text{ and } x=g\). It has local maximum points at \(x=b \text{ and } x=f \) and a local minimum point at \( x=d \).
(a) Find all the values of \(x\) where the graph of \(f\) is increasing. Justify your answer.
(b) Find all the values of \(x\) where the graph of \(f\) has a local maximum. Justify your answer.
(c) Find all the values of \(x\) where the graph of \(f\) has a local minimum. Justify your answer.
(d) Find all the values of \(x\) where the graph of \(f\) has points of inflection and determine which of these is a horizontal point of inflection.
(e) The total area of the region enclosed by graph of \(f'\) and the x-axis for \(a \lt x \lt e\) is 6.
Given that \( f(a) + f(e) = 3 \), find the value of \(f(c)\).
21. | A-Level [402] |
The following equation defines a curve which passes through \( A( 2 \pi ,3 \pi)\)
$$ \sin 2y + y \cos^22x = x + c $$(a) Find the exact value of the constant \( c \).
(b) Find an expression for \( \frac{dy}{dx} \)
(c) Find the equation of the normal to the curve at A, giving your answer in the form \(y = mx + b \)
22. | IB Analysis and Approaches [426] |
Let \(f(x) = \frac{ln3x}{kx} \) where \( x \gt 0\) and \( k \in \mathbf Q^+ \).
(a) Find an expression for the first derivative \(f'(x) \).
The graph of \(f\) has exactly one maximum point at P.
(b) Find the x-coordinate of P.
The graph of \(f\) has exactly one point of inflection at Q.
(c) Find the x-coordinate of Q.
(d) The region enclosed by the graph of \(f\), the x-axis, and the vertical lines through P and Q has an area of one square unit, find the value of \(k\).
23. | IB Studies [208] |
Consider the function \(f(x)=\frac{20}{x^2}+kx\) where \(k\) is a constant and \(x\neq0\).
(a) Write down \(f'(x)\)
The graph of \(y = f(x)\) has a local minimum point at \(x=2\).
(b) Show that \(k=5\).
(c) Find \(f(1)\).
(d) Find \(f'(1)\).
(e) Find the equation of the normal to the graph of \(y=f(x)\) at the point where \(x=1\)
Give your answer in the form \(ay+bx+c=0\) where \(a, b, c \in \mathbb{Z}\)
(f) Sketch the graph of \(y=f(x)\) , for \(-5\le x\le 10\) and \(-10\le y\le 50\).
(g) Write down the coordinates of the point where the graph of \(y=f(x)\) intersects the x-axis.
(h) State the values of \(x\) for which \(f(x)\) is decreasing.
24. | IB Analysis and Approaches [725] |
The north corridor at Addwell High School has a width of \(2 \, \text{m}\). There is a ninety-degree corner at point \(C\). Points \(A\) and \(B\) are variable points on the base of the walls such that \(A\), \(C\), and \(B\) lie on a straight line.
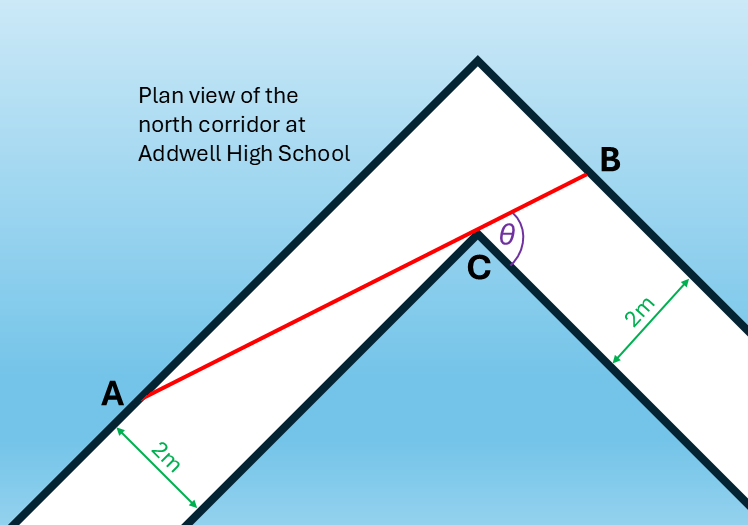
Let \(L\) denote the length \(AB\) in metres.
Let \(\theta\) be the angle that \(AB\) makes with the corridor wall, where \(0 < \theta < \frac{\pi}{2}\).
(a) Find the length of L in terms of \(\theta\).
(b) Find \(\frac{dL}{d\theta}\).
(c) When \(\frac{dL}{d\theta} = 0\), show that \(\theta = \frac{\pi}{4} \).
(d) Find \(\frac{d^2 L}{d\theta^2}\).
(e) Find \(\frac{d^2 L}{d\theta^2}\) when \(\theta = \frac{\pi}{4} \).
(f) Hence, justify that \(L\) is a minimum when \(\theta = \frac{\pi}{4} \).
(g) Determine this minimum value of \(L\).
Two people need to carry a pipe of length \(7 \, \text{m}\) along this corridor. The height of the corridor is \(2.5 \, \text{m}\).
(h) Determine whether this is possible, giving a reason for your answer.
(i) If the width of the pipe is considered to be negligible, what is theoretically the maximum length of a pipe that is able to be carried around the corner of the corridor?
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.