
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher [732] |
Some of the key features of the following graph can be found by using differentiation:
$$ y = 4x^2 - 5x + 9 $$(a) When \( x = 3 \) find the value of \( \dfrac{dy}{dx} \)
(b) Find the coordinates of the point on the graph of \( y = 4x^2 - 5x + 9 \) where the gradient is zero.
(c) When \( y = 5x^p + qx^3 \), \( \quad \dfrac{dy}{dx} = 35x^6 + 30x^2 \)
Find the value of \( p \) and the value of \( q \).
2. | IB Standard [6] |
The acceleration, \(a\) ms-2 , of an object at time \(t\) seconds is given by
$$a=\frac1t+4sin3t, (t\ge1)$$The object is at rest when \(t=1\).
Find the velocity of the object when \(t=7\).
3. | IB Analysis and Approaches [563] |
(a) Find \(\int (4x+5) dx\).
(b) Given \(f'(x) = 4x+5\) find \(f(x)\) if \(f(3.4) = 10.12\).
4. | A-Level [405] |
(a) Find \( \frac{dy}{dx} \) when:
$$ y= (7-5x^2)^{ \frac12 } $$(b) Find the following integral:
$$ \int (1 - cos3x) dx$$5. | IB Analysis and Approaches [574] |
The function \(f\) is defined by \(f(x) = 8 - 5 \sin{x} \), for \( x \ge 0 \).
The diagram shows part of the graph of \(y = f (x) \).
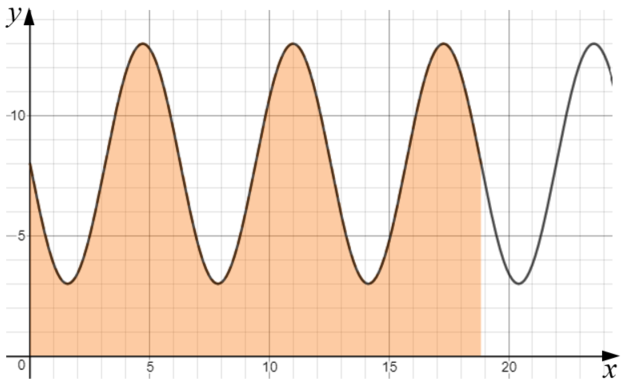
The shaded region is enclosed by the graph of \(y=f(x)\) and the x-axis for the first three periods of the function.
(a) Find the exact value of the x-coordinate of the right side of the shaded region.
(b) Show that the area of the shaded region is \( 48 \pi \).
A hemisphere has a total surface area in square centimetres equal to the shaded area in the previous diagram.
(c) Find the radius of the hemisphere.
6. | IB Applications and Interpretation [446] |
The following diagram shows part of the graph of:
$$f (x) = \frac{(9 + 4x) (6 - x)}{10}, x \in \mathbf R$$The shaded region A is bounded by the x-axis, y-axis and the graph of \(f\).
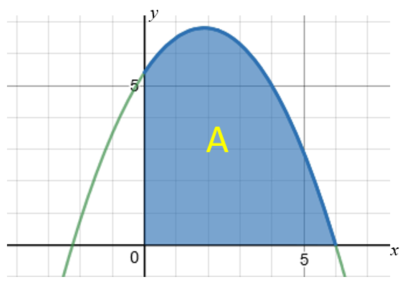
(a) Write down an integral for the area of region A.
(b) Find the area of region A.
The three points A (0 , 0) , B (6 , 9) and C (p , 0) define the vertices of a triangle.
(c) Find the value of p, the x-coordinate of C , such that the area of the triangle is equal to the area of region A.
7. | IB Standard [40] |
Consider the graph of the function \(f(x)=x^2+2\).
(a) Find the area between the graph of \(f\) and the x-axis for \(2\le x \le 3\).
(b) If the area described above is rotated 360o around the x-axis find the volume of the solid formed.
8. | IB Standard [46] |
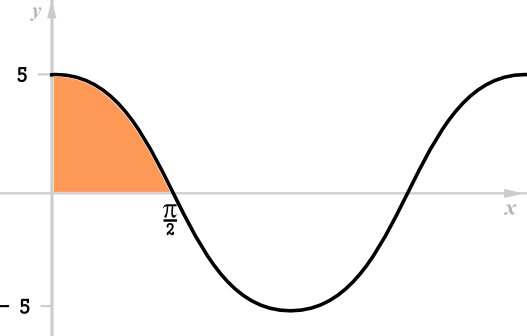
This graph represents the function \(f:x\to a \cos x, a\in \mathbf N\)
(a) Find the value of \(a\).
(b) Find the area of the shaded region.
9. | A-Level [447] |
The diagram shows a sketch of the curve C with equation:
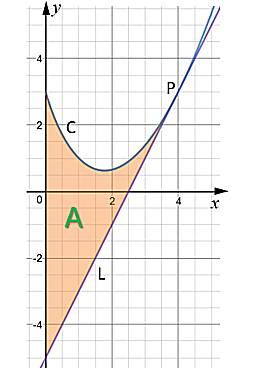 $$ y=2x^{\frac32}-4x+3 $$
$$ y=2x^{\frac32}-4x+3 $$
The point P with coordinates (4, 3) lies on C.
The line L is the tangent to C at the point P.
The region A, shown shaded, is bounded by the curve C, the line L and the y-axis.
Find the area of A making your method clear.
Note that solutions based entirely on graphical or numerical methods are not acceptable.)
10. | IB Analysis and Approaches [426] |
Let \(f(x) = \frac{ln3x}{kx} \) where \( x \gt 0\) and \( k \in \mathbf Q^+ \).
(a) Find an expression for the first derivative \(f'(x) \).
The graph of \(f\) has exactly one maximum point at P.
(b) Find the x-coordinate of P.
The graph of \(f\) has exactly one point of inflection at Q.
(c) Find the x-coordinate of Q.
(d) The region enclosed by the graph of \(f\), the x-axis, and the vertical lines through P and Q has an area of one square unit, find the value of \(k\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.