
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | IGCSE Extended [121] |
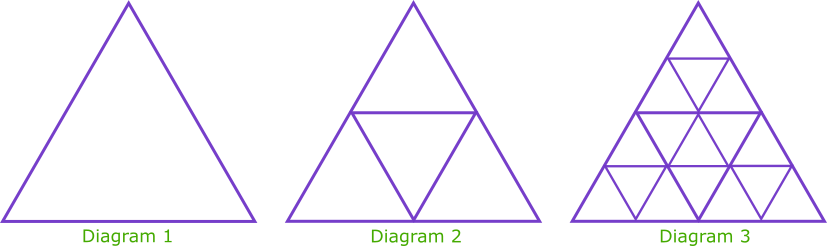
The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre.
In the second diagram there are four triangles each with sides of length \(\frac{1}{2}\) metre.
In the third diagram there are 16 triangles each with sides of length \(\frac{1}{4}\) metre.
(a) Complete this table for more diagrams.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Length of Side | 1 | \(\frac{1}{2}\) | \(\frac{1}{4}\) | |||||
| Power of 2 | 20 | 2-1 | 2-2 |
(b) Complete this table for the number of the smallest triangles in diagrams 4, 5 and 6.
| Diagram 1 | Diagram 2 | Diagram 3 | Diagram 4 | Diagram 5 | Diagram 6 | Diagram \(n\) | ||
| Number of smallest triangles | 1 | 4 | 16 | |||||
| Power of 2 | 20 | 22 | 24 |
(c) Calculate the number of the smallest triangles in the diagram where the smallest triangles have sides of length \(\frac{1}{256}\) metre.
2. | IB Standard [50] |
A square is drawn with sides of length 32 cm. The midpoints of the sides of this square are joined to form a new square and four red triangles. The process is repeated to produce yellow triangles and then again to produce blue triangles.

The length of the equal sides of the red triangles are denoted by \(x_1\) and their areas are each \(A_1\).
The length of the equal sides of the yellow triangles are denoted by \(x_2\) and their areas are each \(A_2\).
The length of the equal sides of the blue triangles are denoted by \(x_3\) and their areas are each \(A_3\).
(a) The following table gives the values of \(x_n\) and \(A_n\), for \(1\le n\le3\). Copy and complete the table.
| \(n\) | 1 | 2 | 3 |
| \(x_n\) | 16 | ||
| \(A_n\) | 128 |
(b) The process of drawing smaller and smaller squares inside each new square is repeated. Find \(A_7\)
(c) Consider an initial square of side length \(k\) cm. The process described above is repeated indefinitely. The total area of one of each colour triangles is \(k\) cm2. Find the value of \(k\).
3. | IB Standard [352] |
The first term of an infinite geometric sequence is 10. The sum of the infinite sequence is 500.
(a) Find the common ratio.
(b) Find the sum of the first 9 terms.
(c) Find the least value of n for which Sn > 250.
4. | IB Analysis and Approaches [739] |
Consider a geometric sequence with first term 2 and common ratio 9.
\(S_n\) is the sum of the first \(n\) terms of the sequence.
(a) Find an expression for \(S_n\) in the form \(\frac{a^n - 1}{b}\), where \(a, b \in \mathbb{Z}^+\).
(b) Hence, show that \(S_1 + S_2 + S_3 + \cdots + S_n = \dfrac{9^{n+1} - 9 - 8n}{32}\).
5. | IB Studies [21] |
Chris checks his Twitter account and notices that he received a tweet at 8:00am. At 8:05am he forwards the tweet to four people. Five minutes later, those four people each forward the tweet to four new people. Assume this pattern continues and each time the tweet is sent to people who have not received it before.
The number of new people who receive the tweet forms a geometric sequence:
$$1 , 4 , …$$(a) Write down the next two terms of this geometric sequence.
(b) Write down the common ratio of this geometric sequence.
(c) Calculate the number of people who will receive the tweet at 8:40am.
(d) Calculate the total number of people who will have received the tweet by 8:40am.
(e) Calculate the exact time at which a total of 5 592 405 people will have received the tweet.
6. | IB Analysis and Approaches [614] |
The sum of the first n terms of a geometric sequence is given by:
$$S_n = \sum_{r=1}^{n} \dfrac{3}{4}\left( \dfrac{5}{7} \right) ^r $$(a) Find the first term of the sequence, \(u_1\).
(b) Find \(S_\infty\).
(c) Find the least value of \(n\) such that \(S_\infty - S_n < 0.001\).
7. | IB Analysis and Approaches [722] |
Consider the arithmetic sequence \( u_1, u_2, u_3, \ldots \).
The sum of the first \( n \) terms of this sequence is given by \( S_n = 2n^2 + n \).
(a) Find the sum of the first six terms.
(b) Given that \( S_7 = 105 \), find \( u_7 \).
(c) Find \( u_1 \).
(d) Hence or otherwise, write an expression for \( u_n \) in terms of \( n \).
Consider a geometric sequence, \( v_n \), where \( v_2 = u_1 \) and \( v_4 = u_7 \).
(e) Find the possible values of the common ratio, \( r \).
(f) Given that \( v_{30} < 0 \), find the value of \( v_5 \).
8. | IB Analysis and Approaches [599] |
The following is an arithmetic sequence: \( \log_7 8 \text{, } \log_7 a \text{, } \log_7 b \text{, } \log_7 64 \) where \(a \gt 1 \text{ and } b \gt 1\)
(a) Show that 8, \(a\), \(b\), and 64 are four consecutive terms of a geometric sequence.
(b) Find the values of \(a\) and \(b\)
9. | IB Standard [498] |
(a) Expand the following as the sum of six terms:
$$ \sum_{r=3}^{8} 2^r$$(b) Find the value of:
$$ \sum_{r=3}^{25} 2^r$$(c) Explain why the following cannot be evaluated:
$$ \sum_{r=3}^{\infty} 2^r$$10. | IB Studies [100] |
Consider the number sequence where \(u_1=500, u_2=519, u_3=538\) and \(u_4=557\) etc.
(a) Find the value of \(u_{30}\)
(b) Find the sum of the first 12 terms of the sequence:
$$\sum_{n=1}^{12} u_n $$Another number sequence is defined where \(w_1=4, w_2=8, w_3=16\) and \(w_4=32\) etc.
(c) Find the exact value of \(w_{10}\).
(d) Find the sum of the first 9 terms of this sequence.
\(k\) is the smallest value of \(n\) for which \(w_n\) is greater than \(u_n\).
(e) Calculate the value of \(k\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.