|
|
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
(a) A function is represented by the following function machine.
A number is input into the machine and the output is used as a new input.
If the second output is 53 work out the number that was the first input.
(b) A number is input into the machine and the output produced is the same number. Work out what this number could have been.
(c) Another function machine is shown below.
If the Input is 2, the Output is 7.
If the Input is 6, the Output is 27.
Use this information to fill in the two boxes.
2. | GCSE Higher |
Here is a function machine that produces two outputs, A and B.
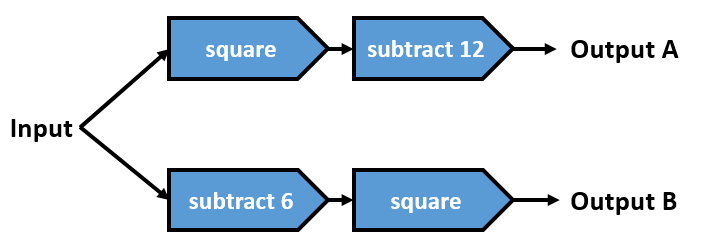
Work out the range of input values for which the output A is less than the output B.
3. | IB Applications and Interpretation |
The circumference of a given circle \(C\) can be represented by the function \(C(A) =2\sqrt{A \pi}, A \ge 0 \) where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 16\).
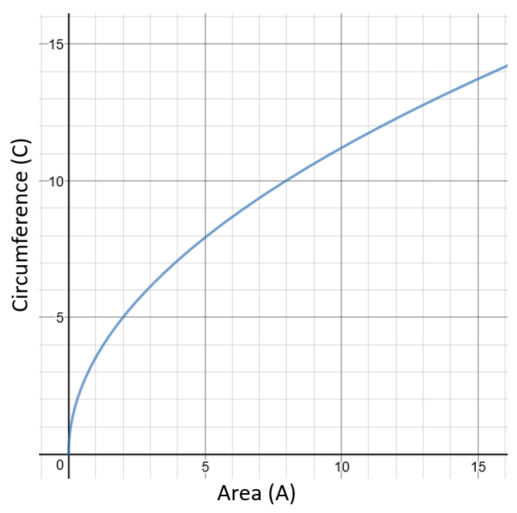
(a) Use the graph to find the value of \(C(8)\) to the nearest whole number.
(b) The range of \(C(A)\) is \(0 \le C(A) \le n\). Write down the value of \(n\).
(c) On the axes above, draw the graph of the inverse function, \(C^{-1}\).
(d) In the context of the question, explain the meaning of \( C^{-1}(12)\).
4. | IB Standard |
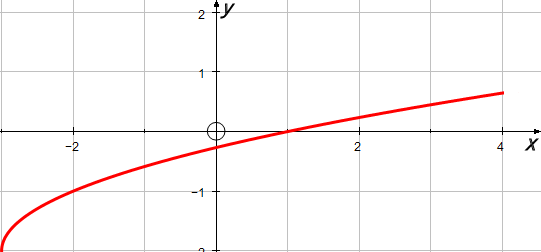
The diagram shows the graph of \(y=f(x)\), for \(-3\le x \le 4\).
The graph passes through the point (4,0.65).
(a) Find the value of \(f(-2)\);
(b) Find the value of \(f^{-1}(0)\);
(c) Find the domain of \(f^{-1}\).
(d) Sketch the graph of \(f^{-1}\).
5. | IB Applications and Interpretation |
The circumference of a given circle \(C\) can be represented by the function \(C(A) = 2 \sqrt{A \pi}\) , \(A \ge 0 \) , where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 10\).
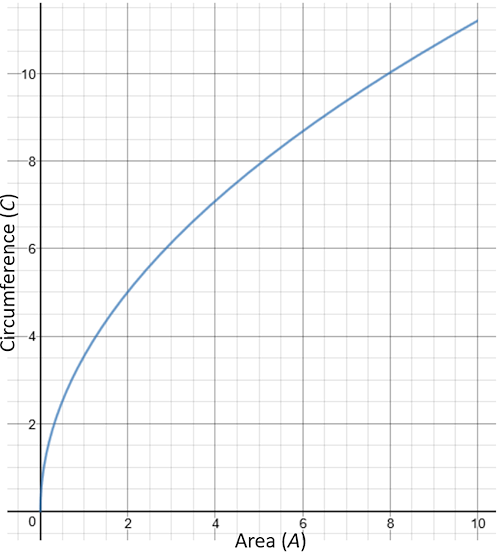
(a) Write down the value of \(C(5)\).
The range of \(C(A)\) is \(0 \le C(A) \le k\).
(b) Find the value of \(k\).
(c) On the axes above, draw the graph of the inverse function, \( C^{-1}\).
(d) In the context of the question, explain the meaning of \( C^{-1}(10) \approx 7.96\).
6. | IB Analysis and Approaches |
Consider the function \(f(x) = k^x \) where \(x, k \in \mathbb{R}\) and \( x \gt 0, k > 1\).
The graph of \(f\) passes through the point \( (\frac{3}{2},27) \).
(a) Find the value of \(k\).
(b) Write down an expression for \( f^{-1}(x) \).
(c) Find the value of \( f^{-1}( \frac{1}{3}) \).
7. | IB Analysis and Approaches |
A function \( g \) is defined by \( g(x) = \frac{3x - 10}{x^2 - 9} \), where \( x \in \mathbb{R} \), \( x \neq \pm3 \).
(a) Determine the range of \( g \).
A function \( h \) is defined by \( h(x) = g(|x|)\sin(t) \), where \( x \in \mathbb{R} \), \( x \neq \pm3 \) and \( t \) is a constant where \( -\pi < t < 0 \).
(b) Find the set of values of \( x \) such that \( h(x) \geq 0 \).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
