|
|
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
The table shows information about the heights of 85 stalagmites.
| Height (\(h\) cm) | Frequency |
|---|---|
| \(10\lt h \le 15\) | 9 |
| \(15\lt h \le 20\) | 13 |
| \(20\lt h \le 25\) | 18 |
| \(25\lt h \le 30\) | 22 |
| \(30\lt h \le 35\) | 15 |
| \(35\lt h \le 40\) | 8 |
(a) Find the class interval that contains the median.
(b) On the grid below, draw a frequency polygon for the information in the table.
2. | GCSE Higher |
The following table shows the time taken by fifty people to answer their emails one day.
| Time, t minutes | Number of people |
| 0 < t ≤ 10 | 5 |
| 10 < t ≤ 20 | 12 |
| 20 < t ≤ 30 | 13 |
| 30 < t ≤ 40 | 15 |
| 40 < t ≤ 50 | 5 |
(a) In which class interval is the median?
(b) How many people took more than 20 minutes?
(c) What is the modal class interval?
(d) Find an estimate for the mean time taken showing all of your working.
3. | GCSE Higher |
The table shows the amount of time, in months, taken to sell houses on the Happyland housing estate.
| Time (m months) | Frequency |
| 0 < m ≤ 2 | 10 |
| 2 < m ≤ 5 | 21 |
| 5 < m ≤ 10 | 25 |
| 10 < m ≤ 15 | 20 |
| 15 < m ≤ 20 | 25 |
(a) Draw a histogram for the information in the table.
(b) Find an estimate for the median.
4. | IB Studies |
The times taken in seconds by a group of students to complete an online exercise are listed as follows.
$$31, 34, 41, 33, 29, 31, 39, 35, 30, 40.$$(a) Find the median time.
(b) Calculate the interquartile range.
(c) Find the probability that a student chosen at random from the group took at least 35 seconds to completed the exercise.
5. | IB Standard |
The personal trainer collected data from a randomly selected sample of days. From this he found that the number glasses of water he drank in a day had a mean of 4.35.
| Glasses | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Frequency | 3 | 5 | 5 | 8 | \(x\) | 7 | 6 |
(a) Find the number of days represented by \(x\)
(b) Write down the standard deviation.
6. | IB Studies |
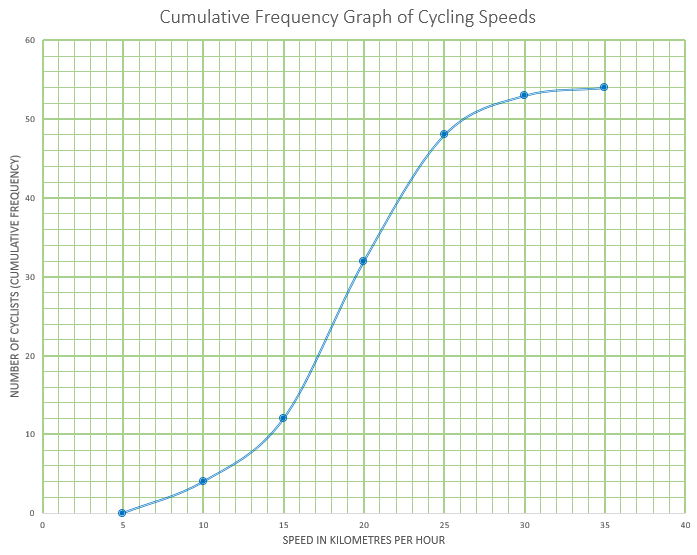
This cumulative frequency graph shows the speeds in kmh-1 of cyclists passing a certain point on a race track.
(a) Estimate the minimum possible speed of one of these cyclists.
(b) Find the median speed of the cyclists.
(c) Write down the 65th percentile.
(d) Calculate the interquartile range.
(e) Find the number of these cyclists that were travelling faster than 22 kmh-1
The table shows the speeds of these cyclists.
| Speed of Cyclists (s) | Number of Cyclists |
|---|---|
| \(0 \lt s \le 5\) | 0 |
| \(5 \lt s \le 10\) | \(a\) |
| \(10 \lt s \le 15\) | 8 |
| \(15 \lt s \le 20\) | 20 |
| \(20 \lt s \le 25\) | 16 |
| \(25 \lt s \le 30\) | 5 |
| \(30 \lt s \le 35\) | \(b\) |
(f) Find the value of \(a\) and of \(b\)
(g) Write down the modal class.
(h) Write down the mid-interval value for the modal class.
(i) Use your graphic display calculator to calculate an estimate of the mean speed of these cyclists.
(j) Use your graphic display calculator to calculate an estimate of the standard deviation of the speeds of these cyclists.
7. | IB Standard |
A data set has \(n\) items. The sum of the items is 650, the mean is 13 and the standard deviation is 5.
(a) Find n.
If each value in the set is multiplied by 7:
(b) Write down the value of the new mean;
(c) Find the value of the new variance.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
