
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
A driving test has two sections, practical(p) and theory(t). One day everyone who took the test passed at least one section. 77% passed the practical section and 81% passed the theory section.
(a) Represent this information on a Venn diagram showing the percentage of candidates in each section of the diagram.

One person is chosen at random from all the people who took the test that day. What is the probability that this person:
(b) passed the practical section, given that they passed the theory section,
(c) passed the theory section, given that they passed only one section?
2. | IB Studies |
Twenty nine children went to a zoo to photograph some animals. The numbers of children who photographed Lions(L), Monkeys(M) and Zebras (Z) are given as follows:
(a) Draw a Venn diagram to show this information.
All of the children photographed at least one of the three types of animal.
(b) Find the number of children that photographed Monkeys and Zebras but not Lions.
(c) Calculate the probability that a child chosen at random from the group photographed a Lion.
(d) Calculate the probability that a child chosen at random from the group photographed only one of the three types of animal.
(e) Calculate the probability that a child chosen at random from the group photographed only Lions, given that they saw only one of the three types of animal.
(f) If a child chosen at random from the group photographed the Lions, find the probability that they also photographed the Monkeys.
3. | IB Studies |
Neal is attending a Scout jamboree in Japan. He has both boots and trainers to wear. He also has the choice of wearing a cap or not.
The probability Neal wears boots is 0.4. If he wears boots, the probability that he wears a cap is 0.7.
If Neal wears trainers, the probability that he wears a cap is 0.25.
The following tree diagram shows the probabilities for Neal's clothing options at the jamboree.

(a) Find the value of A.
(b) Find the value of B.
(c) Find the value of C.
(d) Calculate the probability that Neal wears trainers and no cap.
(e) Calculate the probability that Neal wears no cap.
(f) Calculate the probability that Neal wears trainers given that he is not wearing a cap.
(g) Calculate the probability that Neal wears boots on the first two days of the jamboree.
(h) Calculate the probability that Neal wears boots on one of the first two days, and trainers on the other.
4. | IB Analysis and Approaches |
The time in minutes taken to drive through a city at different times of the day can be modelled by a normal distribution with mean of 45 and standard deviation of 12. A commuter will be late for work if it takes more than an hour to drive through the city.
(a) Find the probability that the commuter is late for work.
(b) Estimate the number of days on which the commuter was late from random sample of 100 days.
(c) Given that the commuter is not late, find the probability that the cross-city journey took less than 25 minutes.
5. | IB Analysis and Approaches |
Events \(A\) and \(B\) are such that \(P(A) = 0.25\), \(P(A|B) = 0.15\) and \(P(A \cup B) = 0.65\).
Find \(P(B)\)
6. | IB Studies |
Julie chooses a cake from a yellow box on a shelf. The box contains two chocolate cakes and three plain cakes. She eats the cake and chooses another one from the box. The tree diagram below represents the situation with the four possible outcomes where C stands for chocolate cake and P for plain cake.
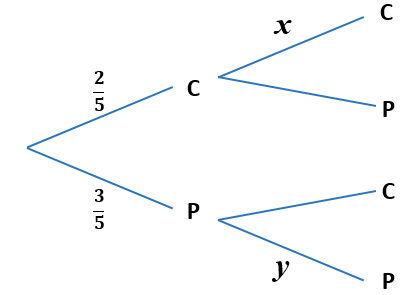
(a) Write down the value of \(x\).
(b) Write down the value of \(y\).
(c) Find the probability that both cakes are plain.
On another shelf there are two boxes, one red and one green. The red box contains four chocolate cakes and five plain cakes and the green box contains three chocolate cakes and four plain cakes. Ben randomly chooses either the red or the green box and randomly selects a cake.
(d) Copy and complete the tree diagram below.
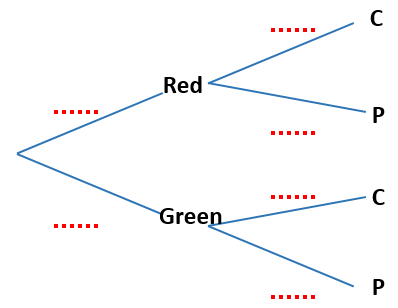
(e) Find the probability that he chooses a chocolate cake.
(f) Find the probability that he chooses a cake from the red box given that it is a chocolate cake.
7. | IB Standard |
Jane and David play two games of golf. The probability that Jane wins the first game is \(\frac56\). If Jane wins the first game, the probability that she wins the second game is \(\frac67\).
If Jane loses the first game, the probability that she wins the second game is \(\frac34\)
(a) Copy and complete the following tree diagram.

(b) Find the probability that Jane wins the first game and David wins the second game.
(c) Find the probability that David wins at least one game.
(d) Given that David wins at least one game, find the probability that he wins both games.
8. | IB Analysis and Approaches |
A factory manufactures switches. It is known that the probability that a switch is found to be defective is 0.04. A random sample of 50 switches is tested.
(a) Find the probability that there is at least one defective switch in the sample.
(b) Given that there is at least one defective switch in the sample, find the probability that there are at least three defective switches.
9. | IB Analysis and Approaches |
At a fitness club, \( 60\% \) of the members are full-time members, and \( 30\% \) of the members participate in group fitness classes. \( 25\% \) of the members are neither full-time members nor participate in group fitness classes.
A member is selected at random.
(a) Find the probability that the member is a full-time member and participates in group fitness classes.
(b) Find the probability that the member participates in group fitness classes, but is not a full-time member.
In the club, \( 50\% \) of the members are male, and \( 40\% \) of the male members participate in group fitness classes.
A member is selected at random. Let \( M \) be the event "the member is male" and let \( F \) be the event "the member participates in group fitness classes".
(c) Find \( P(M \cap F) \).
(d) Determine if the events \( M \) and \( F \) are independent. Justify your answer.

10. | IB Standard |
The weights of players in a sports league are normally distributed with a mean of 75.2 kg, (correct to three significant figures). It is known that 75% of the players have weights between 67 kg and 80 kg. The probability that a player weighs less than 67 kg is 0.05.
(a) Find the probability that a player weighs more than 80 kg.
(b) Write down the standardized value, z, for 67 kg.
(c) Hence, find the standard deviation of weights.
To take part in a tournament, a player's weight must be within 1.5 standard deviations of the mean.
(d) Find the set of all possible weights of players that take part in the tournament.
(e) A player is selected at random. Find the probability that the player takes part in the tournament.
Of the players in the league, 22% are women. Of the women, 60% take part in the tournament.
(f) Given that a player selected at random takes part in the tournament, find the probability that the selected player is a woman.
11. | IB Standard |
Eels are elongated fish, ranging in length from 5cm to 4m. In a certain lake the length of the eels are normally distributed with a mean of 84cm and a standard deviation of 18cm. Eels are classified as giant eels if they are more than 120 cm long.

An eel is selected at random from the lake.
(a) Find the probability that this eel is a giant.
(b) Given that this eel is a giant, find the probability that it is longer than 130cm.
(c) Two eels are selected at random. Find the probability that they are both giants.
100 eels are selected at random.
(d) Find the expected number of these eels that are giants.
(e) Find the probability that at least 5 of these eels are giants.
12. | IB Standard |
Two events A and B are such that \(P(A) = 0.57\) and \(P (A \cap B) = 0.21\).
(a) Find \(P (A \cap B' ) \).
(b) Given that \(P((A \cup B)') = 0.17 \), find \(P(A|B')\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.