
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | IB Standard [6] |
The acceleration, \(a\) ms-2 , of an object at time \(t\) seconds is given by
$$a=\frac1t+4sin3t, (t\ge1)$$The object is at rest when \(t=1\).
Find the velocity of the object when \(t=7\).
2. | IB Standard [79] |
Very accurate equipment was used to measure the movement of a particle which moved in a straight line for 3 seconds. Its velocity, \(v\) ms-1 , at time \(t\) seconds, is given by:
$$v=(t^2-5)^3$$(a) Find the velocity of the particle when \(t=2\).
(b) Find the value of t for which the particle is at rest.
(c) Find the total distance the particle travels during the first three seconds.
(d) Show that the acceleration of the particle is given by \(a=6t(t^2-5)^2\)
(e) Find all possible values of t for which the velocity and acceleration are both positive or both negative.
3. | IB Analysis and Approaches [567] |
A particle moves in a straight line. During the first nine seconds the velocity, \(v\) ms-1 of the particle at time \(t\) seconds is given by:
$$ v(t) = t \cos(t+5) $$
The following diagram shows the graph of v:
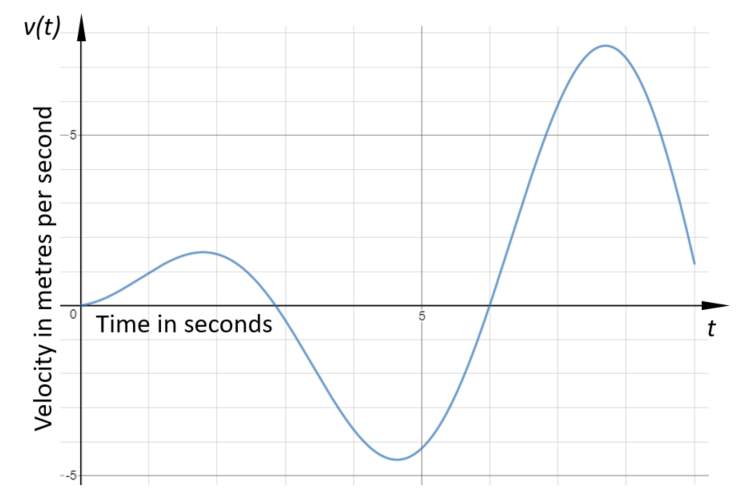
(a) Find the maximum value of \(v\).
(b) Find the acceleration of the particle when t = 6.
(c) Find the total distance travelled by the particle.
4. | IB Analysis and Approaches [756] |
A particle moves in a straight line such that it passes through a fixed point \(O\) at time \(t = 0\), where \(t\) represents time measured in seconds after passing \(O\). For \(0 \le t \le 10\) its velocity, \(v\) metres per second, is given by:
$$v = 3\cos(0.7t) + 0.5t - 2.5$$
The graph of \(v\) is shown in the following diagram.
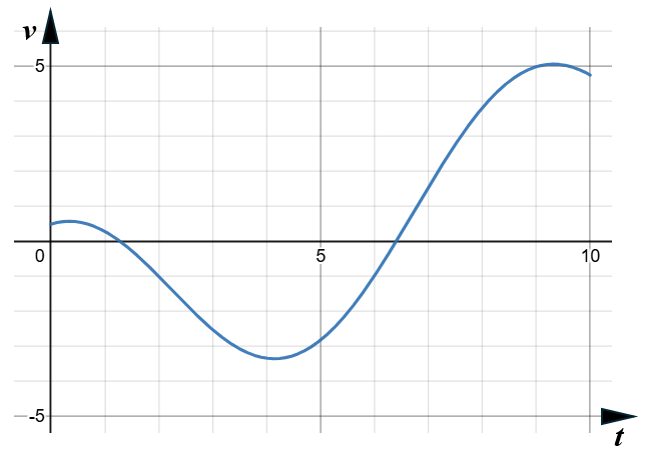
(a) Find the smallest value of \(t\) when the particle changes direction.
The displacement of the particle is measured in metres from \(O\).
(b) Find the range of values of \(t\) for which the displacement of the particle is increasing.
(c) Find the displacement of the particle relative to \(O\) when \(t = 10\).
5. | IB Standard [56] |
Pob and Wie are travelling from Bangkok to Khon Kaen.
Pob travels at a velocity given by \(V_P=50-t^2\), where t is in seconds and the velocity is in ms-1.
Wie's displacement from Bangkok in metres is given by \(S_W=2t^2+70\).
When \(t=0\), both vehicles are at the same point.
Find Pob's displacement from Bangkok when \(t=5\).
6. | IB Analysis and Approaches [573] |
A particle travels in a straight line such that its displacement, \(s\) metres, from a fixed point, \(A\), after \(t\) seconds is given by \(s(t) = t^2 - 5t \), for \( 0 \le t \le 10\), as shown in the following sketch.
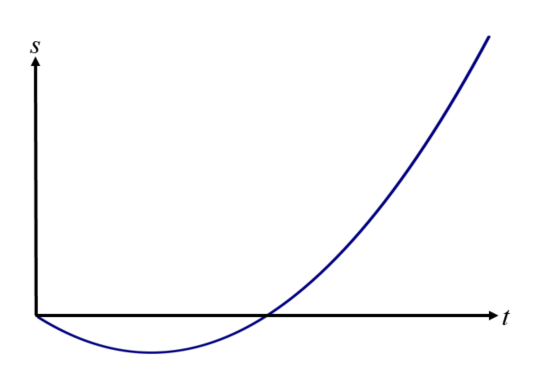
The particle starts at \(A\) and passes through \(A\) again when \(t = q\).
(a) Find the value of \(q\).
The particle changes direction when \(t = r\).
(b) Find the value of \(r\).
(c) Find the displacement of the particle from \(A\) when \(t = r\).
(d) Find distance of the particle from \(A\) when \(t=10\).
(e) Find the total distance travelled by the particle in ten seconds.
A second particle travels along the same straight line such that its velocity is given by \(v(t)=12 - 3t\) for \(t \ge 0\).
When \(t = p\), the distance travelled by this second particle is one metre less than the total distance travelled by the first particle in ten seconds.
(f) Find the value of \(p\)
7. | IB Analysis and Approaches [598] |
A particle P moves along a straight line. The velocity of P is \(v\)ms-l at time \(t\) seconds, where \(v(t) = 5 + 3t - 2t^2\) for \(0 \le t \le 3\). When \(t = 0\), P is at the origin O.
![]() (a) Find the value of \(t\) when P reaches its maximum velocity.
(a) Find the value of \(t\) when P reaches its maximum velocity.
![]() (b) Find the distance of P from O at this time.
(b) Find the distance of P from O at this time.
![]() (c) Sketch a graph of \(v\) against \(t\), clearly showing any points of intersection with the axes.
(c) Sketch a graph of \(v\) against \(t\), clearly showing any points of intersection with the axes.
(d) Find the total distance travelled by P.
8. | IB Standard [32] |
Make a sketch of a graph showing the velocity (in \(ms^{-1}\)) against time of a particle travelling for six seconds according to the equation:
$$v=e^{\sin t}-1$$(a) Find the point at which the graph crosses the \(t\) axis.
(b) How far does the particle travel during these first six seconds?
9. | IB Standard [342] |
A particle P moves along a straight line. The velocity \(v\) in metres per second of P after \(t\) seconds is given by \(v(t) = 3\sin{t} - 8t^{\cos{t}}, 0 \le t \le 7\).
(a) Find the initial velocity of P.
(b) Find the maximum speed of P.
(c) Write down the number of times that the acceleration of P is 0 ms-2.
(d) Find the acceleration of P at a time of 5 seconds.
(e) Find the total distance travelled by P.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.