
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher [292] |
If the universal set is the set of positive even numbers less than 30 and:
$$A = \{4, 8, 12, 16, 20, 24, 28\}$$ $$B = \{6, 12, 18, 24, 28\}$$(a) Complete the Venn diagram with this information.
A number is chosen at random from the universal set.
(b) What is the probability that the number is in the set \(A \cap B\)?
2. | GCSE Higher [583] |
(a) Complete the Venn diagram with the following information.
$$\mathscr{E}= \{1,2,3,4,5,6,7,8,9,10,11,12\}$$ $$A = \{ \text{odd numbers}\}$$ $$B = \{ \text{factors of 24} \}$$(a) Complete the Venn diagram with this information.

A number is chosen at random from the universal set.
(b) What is the probability that the number is in the set \(A \cap B\)?
3. | GCSE Higher [528] |
(a) Complete the Venn diagram to represent this information:
$$\mathscr{E} = \{-4, -3, -2, -1, 0, 1, 2, 3, 4\}$$ $$A = \{1,2,3,4\}$$ $$B = \{-4,-2,2,4\}$$
A number is chosen at random from the universal set \( \mathscr{E} \).
(b) What is the probability that the number is in the set \(A \cap B\)?
4. | GCSE Higher [518] |
The midnight train to Georgia is not the most reliable. The probability that the train will be late on any day is 0.35
(a) Complete the probability tree diagram for Monday and Tuesday.
Monday Tuesday
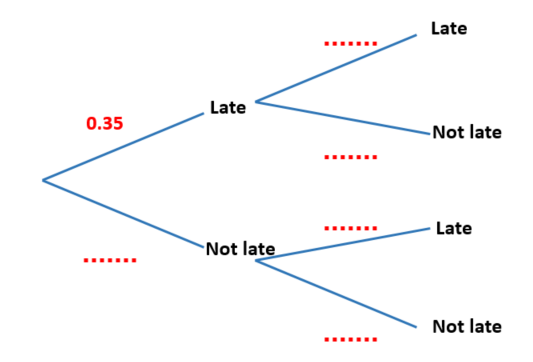
(b) Work out the probability that the train will be late on at least one of these two days.
5. | GCSE Higher [190] |
A driving test has two sections, practical(p) and theory(t). One day everyone who took the test passed at least one section. 77% passed the practical section and 81% passed the theory section.
(a) Represent this information on a Venn diagram showing the percentage of candidates in each section of the diagram.

One person is chosen at random from all the people who took the test that day. What is the probability that this person:
(b) passed the practical section, given that they passed the theory section,
(c) passed the theory section, given that they passed only one section?
6. | GCSE Higher [400] |
The Venn diagram represents a collection of 40 books on sale in an online store.
P represents the books available in paperback format.
D represents the books available in digital format.
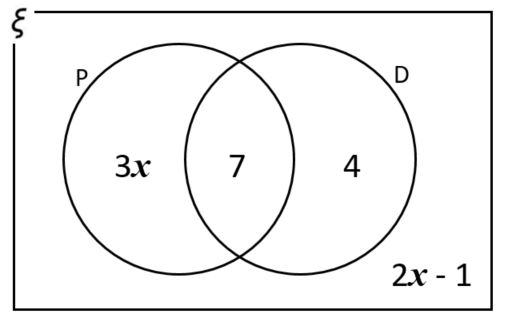
(a) One book from the collection is picked at random. Work out the probability that the book is available in digital format.
(b) One of the books that is available in paperback format is picked at random. Work out the probability that this book is also available in digital format.
7. | GCSE Higher [165] |
A box contains only green and yellow crayons.
Luka takes one crayon at random from the box. The probability that she takes a green crayon is \(\frac16\).
Luka returns the crayon to the bag and adds four more green crayons to the box. The probability that she takes one green crayon at random is now \(\frac14\).
How many crayons of each colour were originally in the box?
8. | GCSE Higher [202] |
Lisa's nephew Sean has two boxes containing plastic building bricks.
A red box contains 5 green bricks and 10 yellow bricks.
A blue box contains 8 green bricks and 16 yellow bricks.
Lisa picks a brick at random from the red box and puts it into the blue box.
Sean now picks a brick at random from the blue box. Show that:
P(Lisa picks a green brick) = P(Sean picks a green brick)
9. | IB Studies [99] |
Twenty nine children went to a zoo to photograph some animals. The numbers of children who photographed Lions(L), Monkeys(M) and Zebras (Z) are given as follows:
(a) Draw a Venn diagram to show this information.
All of the children photographed at least one of the three types of animal.
(b) Find the number of children that photographed Monkeys and Zebras but not Lions.
(c) Calculate the probability that a child chosen at random from the group photographed a Lion.
(d) Calculate the probability that a child chosen at random from the group photographed only one of the three types of animal.
(e) Calculate the probability that a child chosen at random from the group photographed only Lions, given that they saw only one of the three types of animal.
(f) If a child chosen at random from the group photographed the Lions, find the probability that they also photographed the Monkeys.
10. | IB Standard [71] |
Let \(J\) and \(T\) be independent events, where \(P(J)=0.4\) and \(P(T)=0.7\).
(a) Find \(P(J\cap T)\).
(b) Find \(P(J\cup T)\).
(c) Draw a two-set Venn diagram and shade the region that represents \(J\cap T'\).
(d) Find \(P(J\cap T')\).
11. | GCSE Higher [138] |
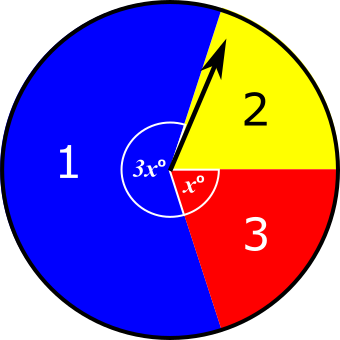
When the arrow is spun once on this spinner, a 1 or a 2 or a 3 can be scored depending on the colour the arrow lands on.
Aimee is going to spin the arrow twice. She will work out her total score by adding the two scores she gets on the two spins. The probability that she will get a total score of 4 is \(\frac{7}{25}\)
Find the value of \(x\).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.