
 |
Exam-Style Questions on VolumeProblems on Volume adapted from questions set in previous Mathematics exams. |
1. | GCSE Higher |
The diagram, not drawn to scale, shows the plan for a large, three dimensional sign which has been ordered to hang outside an ice cream shop.
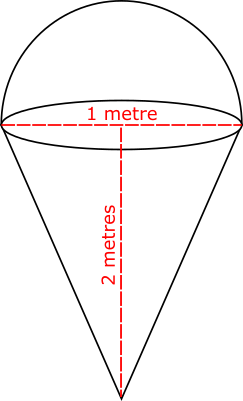
The sign is made of a hemisphere on top of a right cone.
The height of the cone is 2 m.
The top of the cone has a diameter of 1 m.
The hemisphere has a diameter of 1 m.
The total volume of the shape is \(k \pi \) cm3, where \(k\) is an integer.
Work out the value of k.
Where \(r\) is the radius of the sphere.
$$ \text{Volume of a cone} = \frac{\pi r^2 h}{3} $$Where \(r\) is the radius of the circular end of the cone and \(h\) is the height of the cone.
2. | GCSE Higher |
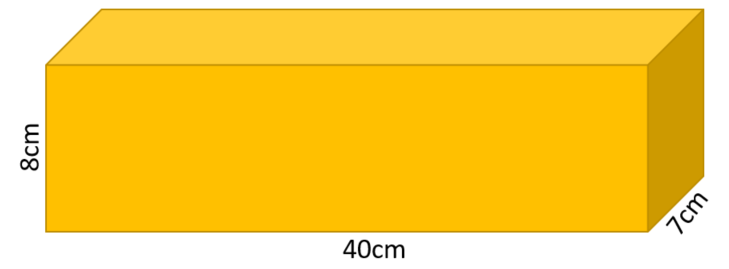
A container is in the shape of a cuboid as shown in the diagram below.
The container is three quarters full of water.
A glass holds 250 ml of water.
What is the greatest number of glasses that can be completely filled with water from the container?
3. | GCSE Higher |
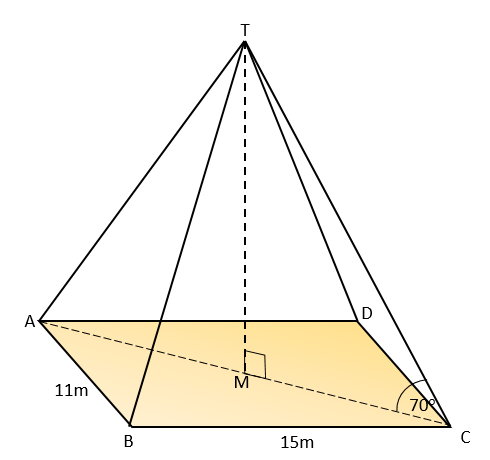
The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale).
The horizontal base ABCD has sides of lengths 11m and 15m. The centre of the base of the pyramid is M.
Angle TMC is 90° and angle TCM is 70°
The volume of a pyramid is \( \frac13 \) × area of base × perpendicular height. Calculate the volume of this pyramid.
4. | GCSE Higher |
The photograph shows a horizontal container for water with a uniform cross-section.
The cross-section is a semicircle.

The radius of the semicircle is 65cm and the length of the container is 3m.
(a) Calculate the volume of water in the container when full.
Yesterday the container was partially filled with water. The greatest depth of the water in the container was 50cm.
(b) Calculate the number of litres of water in the container giving your answer correct to the nearest integer.
5. | IB Applications and Interpretation |
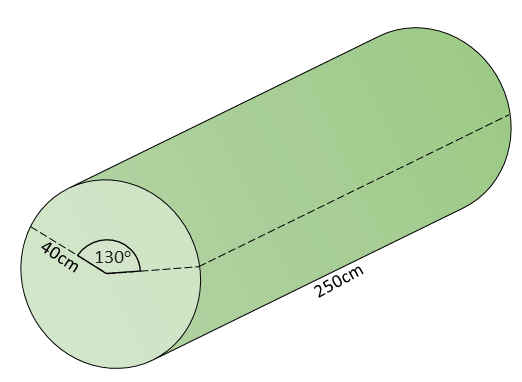
A wedge is to be cut from a log in the shape of a cylinder as shown in the diagram below (not to scale).
The length of the log is 240cm and its radius is 40cm. The cross section of the wedge to be removed is a sector with an angle of 130o.
What is the volume of the remaining piece of the log after the wedge has been removed?
6. | IB Analysis and Approaches |
A function \(f\) is defined as \(f(x) = \arcsin(x — 5)+\frac{\pi}{2}\), where \(4 \le x \le 6 \).
The region bounded by the curve, the y-axis, the x-axis and the line \(y = \pi \) is rotated fully about the y-axis to form a solid of revolution.
Find the volume of the solid.
7. | IB Analysis and Approaches |
The function \( f \) is defined by \( f(y) = \sqrt{y^2 + 10y} \) for \( 0 \leq y \leq 8 \).
The region enclosed by the graph of \( x = f(y) \) and the \( y \)-axis is rotated by \( 360^\circ \) about the \( y \)-axis to form a solid weight. The weight is drilled through from the top along the \( y \)-axis, creating a cylindrical hole 6 units deep. The volume of the remaining weight is 1000 cubic units.
Find the radius of the cylindrical hole that was drilled through the weight.
8. | IB Analysis and Approaches |
The function \( f \) is defined as \( f(x) = \sqrt{x \cos(x^2)} \), where \( 0 \leq x \leq \sqrt{\frac{\pi}{2}} \).
Consider the region \( R \) enclosed by the graph of \( f \) and the x-axis.
The region \( R \) is rotated by \( 2\pi \) radians about the x-axis to form a solid.
Find the exact volume of the solid formed.
9. | IB Analysis and Approaches |
Consider the function \(f(x) = \sec^{-1}(x) \text{ where } 1 \le x \le \frac{\pi}{2} \)
(a) Sketch the curve \(y=f(x)\) clearly indicating the coordinates of the endpoints.
(b) State the domain and range of \( f(x) \).
The curve \(y=f(x) \) is rotated \(2\pi\) about the y-axis to form a solid of revolution that is used to model a flower vase.
(c) Find an expression for the volume, \(Vm^2\), of water in the vase when it is filled to a height of \(h\) metres.
(d) Hence determine the maximum volume of the vase.
At \(t = 0\) the vase is empty. Water is then added to the vase at a constant rate of \(0.1m^3s^{-1} \)
(e) Find the time it takes to fill the vase to Its maximum volume.
(f) Find the rate of change of the height of the water when the vase is filled to half its maximum height.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.