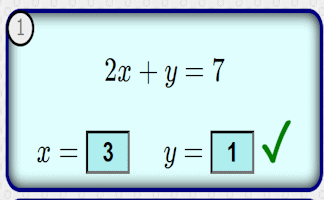Diophantus

Diophantus was a Greek mathematician who lived around 250 AD in Alexandria, Egypt, which was part of the Roman Empire at the time. Not much is known about his life, but he is often referred to as "the father of algebra" because of his work in this area. Diophantus lived during a time when Alexandria was a major center of learning, and he likely had access to a wealth of knowledge and scholarly resources. His work has had a lasting impact on mathematics, even though it was written nearly 1,800 years ago.

Diophantus is best known for his book "Arithmetica," a collection of problems that involve finding integer solutions to equations, now called Diophantine equations. These are equations where only whole numbers are considered as solutions, which is something you might encounter in your maths classes, especially when working with linear equations or number theory. Diophantus's methods for solving these types of problems were very advanced for his time, and many of the techniques he developed are still studied and used by mathematicians today.

Besides his contributions to mathematics, Diophantus may have also influenced other areas of thought, though these are less well-documented. Some historians suggest that his work might have had an impact on the development of early astronomy, as the mathematical techniques he developed could have been useful in solving problems related to the movement of celestial bodies. However, there is little concrete evidence of his involvement in fields outside of mathematics.

Diophantus's work is important because it laid the foundation for algebra as we know it today. By developing ways to solve equations with whole numbers, he opened up new possibilities for mathematicians in both pure and applied mathematics. Learning about Diophantus is important because it helps us understand the origins of many mathematical concepts that are still relevant in the modern world. His contributions have had a lasting influence on the way we approach mathematical problems and continue to be a subject of study and admiration.

There is a riddle about the life of Diophantus which comes from a fifth century Greek anthology of number games and puzzles created by Metrodorus. One of the problems (sometimes called his epitaph) is this riddle.

A classic example of a Diophantine equation is \(3x + 2y = 11\).
The goal is to find values for \(x\) and \(y\) that are whole numbers (integers) and satisfy this equation.

To solve this, we can start by trying different values for \(x\) and see if we can find a corresponding value for \(y\) that makes the equation true. For example, let's try \(x = 1\):

\(3(1) + 2y = 11\)
\(3 + 2y = 11\)
\(2y = 11 - 3\)
\(2y = 8\)
\(y = \frac{8}{2}\)
\(y = 4\)

So, when \(x = 1\), \(y = 4\). Therefore, one solution to the equation is \(x = 1\) and \(y = 4\).

We can check if there are other solutions by trying different values for \(x\). If we try \(x = 2\):

\(3(2) + 2y = 11\)
\(6 + 2y = 11\)
\(2y = 11 - 6\)
\(2y = 5\)

This doesn't give us an integer solution for \(y\), since 5 divided by 2 is 2.5, not a whole number. Therefore, \(x = 2\) doesn't work.

Similarly, if we try \(x = 3\):

\(3(3) + 2y = 11\)
\(9 + 2y = 11\)
\(2y = 11 - 9\)
\(2y = 2\)
\(y = \frac{2}{2}\)
\(y = 1\)

So, another solution is \(x = 3\) and \(y = 1\).

Therefore, the Diophantine equation \(3x + 2y = 11\) has two positive integer solutions:
\((x, y) = (1, 4)\) and \((x, y) = (3, 1)\).

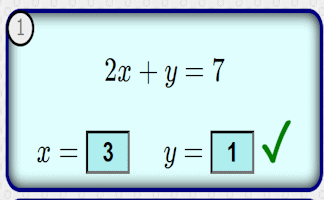
Appreciate the work of Diophantus by trying some of the maths that this mathematician is known for.

There is an activity called Diophantine Equations that you could try right now. Practise finding integer solutions to equations with more than one unknown.

So there's no better time than the present to learn some mathematics from the past: let's Go!

Transum has many activities for the topic 'Algebra' and recommends you try some of them.

Don't put off till tomorrow what you can do today: let's Go!