Constructing, measuring and using geometric notation
Term 3 starting in week 1 :: Estimated time: 3 weeks
- Understand and use letter and labelling conventions including those for geometric figures
- Draw and measure line segments including geometric figures
- Understand angles as a measure of turn
- Classify angles
- Measure angles up to 1800
- Draw angles up to 1800
- Draw and measure angles between 1800 and 3600
- Identify perpendicular and parallel lines
- Recognise types of triangle
- Recognise types of quadrilateral
- Identify polygons up to a decagon
- Construct triangles using SSS
- Construct triangles using SSS, SAS and ASA
- Construct more complex polygons
- Interpret simple pie charts using proportion
- Interpret pie charts using a protractor
- Draw pie charts
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Rotational Symmetry Video This video provides a description of rotational symmetry and shows how I calculate the order of rotational symmetry.
Estimating Angles Estimate the size of the given acute angles in degrees.
Measuring Angles Video Learn how to use a protractor to measure angles of any size. This video is to help you do the online, self-marking exercise.
Measuring Angles Measure the size of the given angles to within two degrees of their actual value.
Snowflake Generator See how the hexagon can be transformed into a snowflake with some basic translations.
Xmas Symmetry Pairs Match the pictures with the description of their symmetry.
Pie Charts Develop the skills to construct and interpret pie charts in this self-marking set of exercises.
Polygon People Name the polygons and other geometrical shapes that make up the Polygon People.
Polygons Name the polygons and show the number of lines and order of rotational symmetry.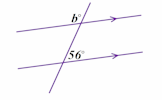
Angle Parallels Understand and use the relationship between parallel lines and alternate and corresponding angles.
Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings.
Polygon Angles Animation Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
Rotational Symmetry Pairs The traditional pairs or pelmanism game adapted to test knowledge of rotational symmetry.
Shapes In The Stars Join up the stars to find the hidden regular polygons.
Polygon Angles Video A concise reminder about angles, both interior and exterior, in regular and irregular polygons.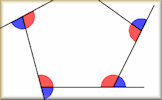
Polygon Angles A mixture of problems related to calculating the interior and exterior angles of polygons.
Tessellations Drag the shapes onto the canvas to create tessellating patterns then try the tessellations quiz.
Polygon Pieces Arrange the nine pieces of the puzzle on the grid to make different polygons.
Constructions Construct the diagrams from the given information then check your accuracy.
Polygon Properties Connect the names of the polygons with the descriptions of their properties.
The Great Dodecahedron Pupils are not allowed to use their hands to point but must describe fully any shapes they can see in this picture.
Symmetry Table Challenge In how many cells can you draw symmetrical shapes with the given row and column headings?
Ruler and Compass Constructions Video A demonstration of standard ruler and compass constructions.
Geometry Toolbox Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.
Polygon Hunting Find all the polygons that can be drawn by joining dots on this seven dot grid.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Angles Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles. Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them. Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
- Construction In a way this topic is quite different to all of the other topics in school mathematics. It requires a practical skill as well as the understanding of the geometrical concepts. It also requires a sharp pencil, a sturdy ruler and a decent pair of compasses. Younger children should practise using the drawing instruments to make patterns. They will then progress to constructing accurate diagrams, plans and maps. Older pupils are taught to derive and use the standard ruler and compass constructions for the perpendicular bisector of a line segment, the perpendicular to a given line from a given point and the bisector of a given angle.
- Geometry Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of a formal mathematical science emerging in the West as early 6th Century BC. See also the topics of Angles, Area, Bearings, Circles, Enlargements, Mensuration, Pythagoras, Shape, Shape (3D), Symmetry, Transformations and Trigonometry.
- Loci A locus (plural: loci) is a set of points whose location satisfies or is determined by one or more specified conditions. This topic links to Geometry and Shape and provides opportunity for accurate drawing and 'people maths' where pupils can position themselves in the classroom according to certain conditions.
- Shape This topic is aimed at the learners of basic geometry, which is the study of size, shape and position. More than other areas of mathematics this topic helps pupils to learn about the definitions and properties of basic shapes. There are many activities provided ranging from simple shape naming games to applying more advanced formulas and theorems. The most popular activities however are those involving pupils to count the number of triangles or rectangles in patterns and come up with effective strategies and justifications for their answers. The work pupils produce for this topic can make very good display material. The use of colour can enhance the diagrams and make the learning environment more conducive to study. There are many connections between the mathematics of shape and Art. There are fascinating works of art based on symmetry, tessellations and transformations.
- Symmetry This topic covers line symmetry and rotational symmetry. The innate appeal of symmetry can be found in our reactions to finding symmetry in natural objects, such as precisely formed crystals or seashells. Symmetry in art is another source of delight. Understanding the mathematics of symmetry is the focus of this topic. Accurately drawing the reflection of an object requires an understanding of the relative positions of reflected points. Defining the position of the mirror line is important to find the position and orientation of the reflection. The Wrapping Paper lesson starter makes it clear that for rotational symmetry, the position of the centre of rotation is very important. Work on this topic can produce some excellent display work!
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Angle Estimates
Estimate the sizes of each of the angles then add your estimates together.
2nd Lesson
Sectors
Work out which sectors fit together to make complete circles. Knowledge of the sum of the angles at a point will help find more than one correct solution to this puzzle.
3rd Lesson
Pie Chart
An exercise in estimating what the sectors of a pie chart represent.
4th Lesson
Area Two
How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
5th Lesson
How Many Triangles? 1
How many Triangles can you find in the diagram?
6th Lesson
How Many Squares? 2
How many squares can be found by joining four dots on the grid?
7th Lesson
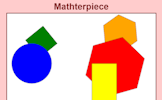
Mathterpiece
Memorise a picture made up of geometrical shapes
8th Lesson
Square Circle Kite
Write down the names of all the mathematical shapes you know.
9th Lesson
Overlapping Squares
If two squares overlap, what shapes can the overlapping region make?
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
