Properties of shape
Term 3 starting in week 1 :: Estimated time: 3 weeks
- Measure with a protractor
- Draw lines and angles accurately (review)
- Introduce angles (review)
- Angles on a straight line (review)
- Angles around a point (review)
- Calculate angles
- Vertically opposite angles
- Angles in a triangle
- Angles in a triangle - special cases
- Angles in a triangle - missing angles
- Angles in special quadrilaterals
- Angles in regular polygons
- Draw shapes accurately
- Draw nets of 3-D shapes
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Angle Points Video See a demonstration of angles in a full turn around a point, angles together on a straight line and vertically opposite angles.
Nets Video Learn more about three-dimensional shapes and their nets.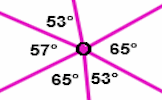
Angle Points Apply the properties of angles at a point, angles on a straight line and vertically opposite angles.
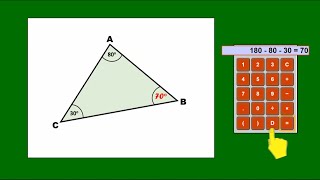Angles in a Triangle Video A reminder of how to use the fact that the angles in a triangle sum to 180 degrees to find the size of unmarked angles in triangular diagrams.
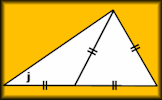Angles in a Triangle A self marking exercise involving calculating the unknown angle in a triangle.
Different types of Triangle Euclid and his friends explain how many different kinds of triangle there are.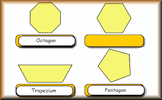
Polygons Name the polygons and show the number of lines and order of rotational symmetry.
Angle Chase Find all of the angles on the geometrical diagrams.
Scale Drawings Measure line segments and angles in geometric figures, including interpreting scale drawings.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Net or Not Drag the nets into the corresponding panels to show whether they would fold to form a cube.
Dice Net Challenge Drag the numbers onto the net so that when it is folded to form a cube numbers on opposite faces add up to prime numbers.
Cube Face Meetings Visualise the cubes formed by the nets and paint the three faces meeting at a vertex.
Cubical Net Challenge Find all the ways of painting the faces of cubes using only two colours.
Coloured Cube 3D Colour in the remaining faces of the nets of the cubes to match the rotating three-dimensional picture.
Online Logo An online version of the Logo programming language with 30 mathematical challenges.
Area shapes Investigate polygons with an area of 4 square units. This is your starting point, you can decide how to proceed.
Polygon Angle Explorer Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
Shapes In The Stars Join up the stars to find the hidden regular polygons.
Polygon Angles Video A concise reminder about angles, both interior and exterior, in regular and irregular polygons.
Polygon Angles A mixture of problems related to calculating the interior and exterior angles of polygons.
Tessellations Drag the shapes onto the canvas to create tessellating patterns then try the tessellations quiz.
Plans and Elevations Interpret plans and elevations of three dimensional shapes.
Polygon Pieces Arrange the nine pieces of the puzzle on the grid to make different polygons.
Polygon Profiles A visual aid about the properties of regular polygons designed to be projected onto a whiteboard for whole class exposition.
Polybragging The Transum version of the Top Trumps game played online with the properties of polygons.
Constructions Construct the diagrams from the given information then check your accuracy.
Polygon Properties Connect the names of the polygons with the descriptions of their properties.
Faces, Edges and Vertices Calculate the number of faces, edges and vertices on 3D Shapes.
Platonic Solids Identify the names, nets and features of the five regular polyhedra.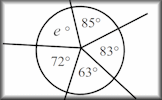
Angles Mixed Find the unknown angles by using the basic angle theorems.
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Ruler and Compass Constructions Video A demonstration of standard ruler and compass constructions.
Geometry Toolbox Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.
Polygon Hunting Find all the polygons that can be drawn by joining dots on this seven dot grid.
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Angles Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles. Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them. Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
- Construction In a way this topic is quite different to all of the other topics in school mathematics. It requires a practical skill as well as the understanding of the geometrical concepts. It also requires a sharp pencil, a sturdy ruler and a decent pair of compasses. Younger children should practise using the drawing instruments to make patterns. They will then progress to constructing accurate diagrams, plans and maps. Older pupils are taught to derive and use the standard ruler and compass constructions for the perpendicular bisector of a line segment, the perpendicular to a given line from a given point and the bisector of a given angle.
- Shape This topic is aimed at the learners of basic geometry, which is the study of size, shape and position. More than other areas of mathematics this topic helps pupils to learn about the definitions and properties of basic shapes. There are many activities provided ranging from simple shape naming games to applying more advanced formulas and theorems. The most popular activities however are those involving pupils to count the number of triangles or rectangles in patterns and come up with effective strategies and justifications for their answers. The work pupils produce for this topic can make very good display material. The use of colour can enhance the diagrams and make the learning environment more conducive to study. There are many connections between the mathematics of shape and Art. There are fascinating works of art based on symmetry, tessellations and transformations.
- Shape (3D) A particular skill is required to be able to excel in this area of Mathematics. Spatial awareness is important for solving multi-step problems that arise in areas such as architecture, engineering, science, art, games, and everyday life. Children have varying abilities visualizing three dimensional relationships but these abilities can be developed through practical activities and working through mathematical problems. Breaking down three dimensional situations into smaller two dimensional parts in an important strategy for problem solving. See also the "Shape" Starters.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Angle Estimates
Estimate the sizes of each of the angles then add your estimates together.
2nd Lesson
Sectors
Work out which sectors fit together to make complete circles. Knowledge of the sum of the angles at a point will help find more than one correct solution to this puzzle.
3rd Lesson
Square Angles
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.
4th Lesson
Dice Reflections
A dice is reflected in two mirrors. What numbers can be seen?
5th Lesson
Dice Nets
Determine whether the given nets would fold to produce a dice.
6th Lesson
Faces and Edges
Find the number of faces, edges and vertices on some familiar objects.
7th Lesson
Icosahedron
How many triangles are there on the surface of a regular icosahedron.
8th Lesson
Get A Wiggle On
A mixture of calculations to get your brain working at the start of a mathematics lesson.
9th Lesson
Refreshing Revision
It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
