Developing geometric reasoning
Term 3 starting in week 4 :: Estimated time: 3 weeks
- Understand and use the sum of angles at a point
- Understand and use the sum of angles on a straight line
- Understand and use the equality of vertically opposite angles
- Know and apply the sum of angles in a triangle
- Know and apply the sum of angles in a quadrilateral
- Solve angle problems using properties of triangles and quadrilaterals
- Solve complex angle problems
For higher-attaining pupils:
- Find and use the angle sum of any polygon
- Investigate angles in parallel lines
- Understand and use parallel line angle rules
- Use known facts to obtain simple proofs
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Angle Points Video See a demonstration of angles in a full turn around a point, angles together on a straight line and vertically opposite angles.
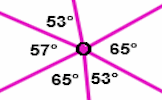Angle Points Apply the properties of angles at a point, angles on a straight line and vertically opposite angles.
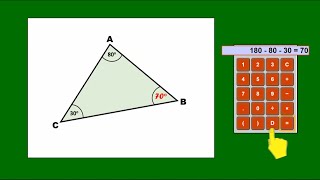Angles in a Triangle Video A reminder of how to use the fact that the angles in a triangle sum to 180 degrees to find the size of unmarked angles in triangular diagrams.
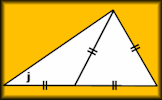Angles in a Triangle A self marking exercise involving calculating the unknown angle in a triangle.
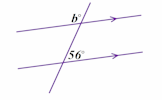Angle Parallels Understand and use the relationship between parallel lines and alternate and corresponding angles.
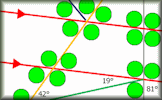Angle Chase Find all of the angles on the geometrical diagrams.
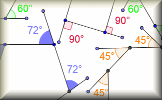Angle Theorems Diagrams of the angle theorems with interactive examples.
Polygon Angles Animation Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
Polygon Angles Video A concise reminder about angles, both interior and exterior, in regular and irregular polygons.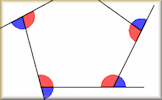
Polygon Angles A mixture of problems related to calculating the interior and exterior angles of polygons.
Polybragging The Transum version of the Top Trumps game played online with the properties of polygons.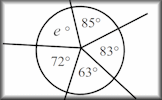
Angles Mixed Find the unknown angles by using the basic angle theorems.
Geometry Toolbox Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.
Polygon Hunting Find all the polygons that can be drawn by joining dots on this seven dot grid.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Angles Pupils should understand that angles represent an amount of turning and be able to estimate the size of angle. When constructing models and drawing pupils should be able to measure and draw angles to the nearest degree and use appropriate language associated with angles. Pupils should know the angle sums of polygons and that of angles at a point and on a straight line. They will learn about angles made in circles by chords, radii and tangents and recognise the relationships between them. Pupils will work with angles using trigonometry, transformations and bearings. In exams pupils are often instructed that while non-exact answers should be given to three significant figures, angle answers should be given to one decimal place.
- Bearings A bearing is a description of a direction. It is the number of degrees measured in a clockwise direction from north as seen from above. Convention, probably born out of the need to be quite clear when saying a bearing over a crackly aircraft radio or storm at sea, three figures are given for each bearing. So 90 degrees would be expressed as 090 degrees. The four main directions are known as the cardinal points. These are north (360°), east (090°), south (180°) and west (270°). The directions in between those are known as the half cardinal points and can be expressed as north-east (045°), south-east (135°), south-west (225°) and north west (315°). The study of bearings in Mathematics provides a practical, real-life application of angles and geometry. It can provide a need for numerical calculations, scale drawing and estimation.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Hexagon
On a full page in the back of your exercise book draw a perfectly regular hexagon.
2nd Lesson
Pentagon
On a full page in the back of your exercise book draw a perfectly regular pentagon.
3rd Lesson
Square Angles
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.
4th Lesson
Air Traffic Control
Work out which aircraft are in danger of colliding from their positions and direction of travel. An exercise in understanding bearings.
5th Lesson
Mental Maths Test
The starter is a PowerPoint file containing a twenty question mental arithmetic test. It will advance from one question to the next automatically.
6th Lesson
Breathe Easily
How many breaths have you taken in your lifetime?
7th Lesson
Six of the Best
Six calculations to perform without a calculator.
8th Lesson
Not Too Close
This activity requires eight students to sit non consecutively on a grid of chairs.
9th Lesson
Step Perimeter
Is it possible to work out the perimeter of this shape if not all the side lengths are given?
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
