Sets and probability
Term 3 starting in week 9 :: Estimated time: 2 weeks
- Identify and represent sets
- Interpret and create Venn diagrams
- Understand and use the intersection of sets
- Understand and use the union of sets
- Know and use the vocabulary of probability
- Generate sample spaces for single events
- Calculate the probability of a single event
- Understand and use the probability scale
- Know that the sum of probabilities of all possible outcomes is 1
For higher-attaining pupils:
- Understand and use the complement of a set
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Venn Worksheet A collection of worksheets all related to the regions in Venn diagrams and the set notation describing them (answers included)
Probability Words A visual aid to highlight the vocabulary of probability and to debate the relationship between the given words.
Probability Washing Line Hang out the washing on the line so that the probability words on the t-shirts are in order.
Pin Drop Estimate the probability of a drawing pin landing point up from experimental data.
Likelihood Arrange some statements in order according to the probability of them happening. Compare your opinion with thousands of others.
Probability Video A reminder of how to work out basic probability leading to simple combined events and expected values.
Probability Basic probability questions in an online exercise.
Hi-Low Predictions A version of the Play Your Cards Right TV show. Calculate the probabilities of cards being higher or lower.
Human Venn Diagrams Pupils move to positions in large circles on the floor according to their personal data.
Dice Investigation Throw two dice and multiply the scores. Investigate the different products you can obtain. What about adding? What about using three dice?
Snail Race Projectable Twelve snails have a race based on the sum of two dice. This is the teachers' version of the race simulation.
Snail Race A race between 12 snails. Which snail is most likely to win? This is the students' version of the race simulation.
Two Dice Possibility Space An interactive visual aid showing the possibility space obtained when throwing two dice
Venn Totals Practise reading and creating Venn diagrams containing two and three sets and the number of elements in those sets.
Dice Bingo Choose your own numbers for your bingo card. The caller uses two dice and adds the numbers together.
Frequency Trees Use a frequency tree to show two or more events and the number of times they occurred.
Set Notation Matching Match the set notation statements with the equivalent symbol. A drag and drop self-marking exercise.
Venn Paint Video Here is a demonstration of how to illustrate union, intersection and complement of sets as they appear in Venn diagrams.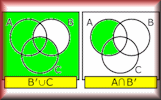
Venn Paint Flood fill the regions of the Venn diagrams according to the given statements.
Venn Diagram Pairs The traditional pairs or pelmanism game adapted to test knowledge of Venn diagrams.
The Maths of Gambling Gambling is never a good idea and this activity might help you understand the mathematics involved.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Combinations "A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange." - Wikipedia In Primary school pupils should practise sorting and grouping items noting similarities and differences. They should develop strategies for finding all the ways a small number of items can be arranged so that missing or duplicates can be found quickly. By the end of Secondary school pupils will have learnt the formulas for combinations and permutations and apply them when solving probability problems.
- Probability Probability is a measure of the weight of evidence, and is arrived at through reasoning and inference. In simple terms it is a measure or estimation of likelihood of the occurrence of an event. The word probability comes from the Latin word probabilitas which is a measure of the authority of a witness in a legal case. Some of the earlier mathematical studies of probability were motivated by the desire to be more profitable when gambling. Today however the practical uses of probability theory go far beyond gambling and are used in many aspects of modern life. We believe that even adults can, in many cases, have a poor intuition regarding the effects of probability. These activities are designed to help pupils calculate but also get a 'feel' for the principles of probability.
- Sets Understand the terminology of sets and the basic set operations. Learn about Venn diagrams and the use of sets in the real world.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Venn Diagram
Arrange numbers on the Venn Diagram according to their properties.
2nd Lesson
Coloured Sheep
What is the probability of picking a red sheep from the sheep in the field?
3rd Lesson
Pick From The Pot
The pot contains 10 counters which are being randomly removed and replaced. How many of each colour do you think are in the pot?
4th Lesson
Ice Cream
How many different ice cream cones can be made by choosing two scoops from six flavours?
5th Lesson
Bus Stop
How many different ways can four people stand in line?
6th Lesson
Kim's Game 2
This is the Maths version of the traditional memory game. Memorise 10 mathematical facts then recall them as they disappear from view.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
