Area of trapezia and circles
Term 3 starting in week 4 :: Estimated time: 2 weeks
- Calculate the area of triangles, rectangles and parallelograms (review)
- Calculate the area of a trapezium
- Calculate the perimeter and area of compound shapes (1)
- Investigate the area of a circle
- Calculate the area of a circle and parts of a circle without a calculator
- Calculate the area of a circle and parts of a circle with a calculator
- Calculate the perimeter and area of compound shapes (2)
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Area and Perimeter of a Rectangle Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
Area Builder An interactive workspace in which to make shapes using square tiles with given areas and perimeters.
Area and Perimeter of a Parallelogram Many different ways to practise your skills finding the areas and perimeters of parallelograms.
Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.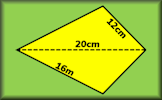
Area and Perimeter of a Kite A short exercise to practise using the formulae for area and perimeter of a kite.
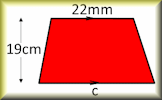Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
Area and Perimeter Show that you know the area and perimeter formulas of basic shapes.
Area Maze Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.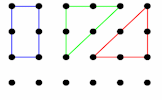
Area Two How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
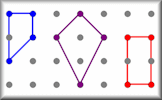Quad Areas Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Circles Area and Circumference Video The circumference and area of a circle can be found if the radius or diameter are known.
Circles Practise using pi to calculate various circle measurements. There are six levels of difficulty.
Pi Some information about Pi, the "celebrity number'. A video features maths-loving author Alex Bellos.
Areas of Composite Shapes Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.
Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes.
Heron's Formula Use the lengths of the three sides of a triangle to calculate the area.
Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Pi and Four Fingers Why is The Simpsons not in Base 8? In this video Simon Singh talks about Pi and Maths in The Simpsons cartoon.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Area Pupils should not only be able to remember and apply area formulae but they should also have a good understanding of what area means. This can be achieved by beginning the study of area with plenty of practical examples. The Pin Board provides an open-ended interactive experimental environment to secure a good fundamental understanding of area. Some examinations provide formulae sheets but it is still important that pupils know the common formulas for finding the areas of basic shapes. They should use these formulae in context to find areas of basic and compound shapes and be able to give answers using appropriate units. Pupils will also learn to find the surface areas of three dimensional shapes, use scale to determine areas from maps and solve real world problems involving areas. See also the topics called Measures, Shape (3D) and Ratio.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.
- Mensuration Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume. It is linked closely to the topic of Estimation and related to the topics of Angles, Shape and Shave (3D). It is essential for pupils to have an understanding of the units used to measure which include both the more common metric units and the Imperial units still in common usage. We have found a good teaching strategy is to ask each of the pupils to "Bring to the next Maths lesson some visual aid which will help the rest of the class remember the size of a unit of measurement". See Memorable Measures below for the printable resources. This activity provides an association with a unit, a visual aid and a known person which is a great memory enhancer.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Icosahedron
How many triangles are there on the surface of a regular icosahedron.
2nd Lesson
Tool Triangle
Place the numbers on the triangle so that the totals along each of the sides are equal.
3rd Lesson
May Day
Add together the dates of all the Thursdays in May this year. Which day sum is largest?
4th Lesson
Meta Products
Which numbers when multiplied by the number of letters in the word(s) of the number give square numbers?
5th Lesson
News Common
Follow the compass directions given in the squares to find where the route starts?
6th Lesson
One one
Continue the given number pattern with the help of a little lateral thinking.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
