Three-dimensional shapes
Term 1 starting in week 7 :: Estimated time: 3 weeks
- Know names of 2-D and 3-D shapes
- Recognise prisms
- Accurate nets of cuboids and other 3-D shapes
- Sketch and recognise nets of cuboids and other 3-D shapes
- Plans and elevations
- Find area of 2-D shapes (review)
- Surface area of cubes and cuboids
- Surface area of triangular prisms
- Surface area of a cylinder
- Volume of cubes and cuboids
- Volume of other 3-D shapes - prisms and cylinders
For higher-attaining pupils:
- Explore volumes of cones, pyramids and spheres
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Area and Perimeter of a Rectangle Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
Area and Perimeter of a Parallelogram Many different ways to practise your skills finding the areas and perimeters of parallelograms.
Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.
Nets Video Learn more about three-dimensional shapes and their nets.
Drawing 3D Objects Draw two-dimensional representations of three-dimensional objects on an isometric dotty grid.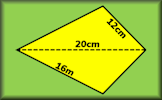
Area and Perimeter of a Kite A short exercise to practise using the formulae for area and perimeter of a kite.
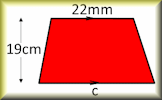Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
Area and Perimeter Show that you know the area and perimeter formulas of basic shapes.
Area Two How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
Quad Areas Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Net or Not Drag the nets into the corresponding panels to show whether they would fold to form a cube.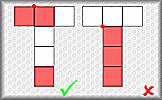
Cube Face Meetings Visualise the cubes formed by the nets and paint the three faces meeting at a vertex.
Cubical Net Challenge Find all the ways of painting the faces of cubes using only two colours.
Coloured Cube 3D Colour in the remaining faces of the nets of the cubes to match the rotating three-dimensional picture.
Plans and Elevations Interpret plans and elevations of three dimensional shapes.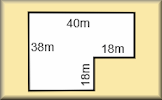
Areas of Composite Shapes Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.
Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes.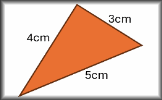
Heron's Formula Use the lengths of the three sides of a triangle to calculate the area.
Faces, Edges and Vertices Calculate the number of faces, edges and vertices on 3D Shapes.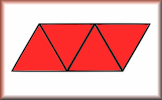
Platonic Solids Identify the names, nets and features of the five regular polyhedra.
Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.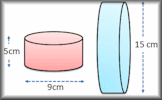
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Area Pupils should not only be able to remember and apply area formulae but they should also have a good understanding of what area means. This can be achieved by beginning the study of area with plenty of practical examples. The Pin Board provides an open-ended interactive experimental environment to secure a good fundamental understanding of area. Some examinations provide formulae sheets but it is still important that pupils know the common formulas for finding the areas of basic shapes. They should use these formulae in context to find areas of basic and compound shapes and be able to give answers using appropriate units. Pupils will also learn to find the surface areas of three dimensional shapes, use scale to determine areas from maps and solve real world problems involving areas. See also the topics called Measures, Shape (3D) and Ratio.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.
- Mensuration Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume. It is linked closely to the topic of Estimation and related to the topics of Angles, Shape and Shave (3D). It is essential for pupils to have an understanding of the units used to measure which include both the more common metric units and the Imperial units still in common usage. We have found a good teaching strategy is to ask each of the pupils to "Bring to the next Maths lesson some visual aid which will help the rest of the class remember the size of a unit of measurement". See Memorable Measures below for the printable resources. This activity provides an association with a unit, a visual aid and a known person which is a great memory enhancer.
- Shape (3D) A particular skill is required to be able to excel in this area of Mathematics. Spatial awareness is important for solving multi-step problems that arise in areas such as architecture, engineering, science, art, games, and everyday life. Children have varying abilities visualizing three dimensional relationships but these abilities can be developed through practical activities and working through mathematical problems. Breaking down three dimensional situations into smaller two dimensional parts in an important strategy for problem solving. See also the "Shape" Starters.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Faces and Edges
Find the number of faces, edges and vertices on some familiar objects.
2nd Lesson
Dice Nets
Determine whether the given nets would fold to produce a dice.
3rd Lesson
Wordles
Turn mathematical words into designs which will help you remember the meanings of the words.
4th Lesson
Four Gone
An activity involving a broken calculator which is missing the four button. Can you evaluate the given expressions without using the four?
5th Lesson
How Many Triangles? 2
How many triangles are hidden in the pattern? What strategy might you use to count them all to ensure you don't miss any out?
6th Lesson
Simple Nim
The classic game of Nim played with a group of pens and pencils. The game can be extended to the multi-pile version.
7th Lesson
Maggots
Do as many of the calculations as possible before the maggots infest!
8th Lesson
Dimidiate
Arrange the digits from 1 to 9 in alphabetical order. How many times can this number be halved?
9th Lesson
Firewords
Find words which cost 100p if A costs 1p, B costs 2p etc
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
