Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Scale Factors Video The scale factor, area factor and volume factor of similar shapes are quite different.
Scale Factors Video The scale factor, area factor and volume factor of similar shapes are quite different.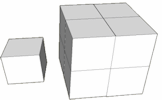 Similar Shapes Questions about the scale factors of lengths, areas and volumes of similar shapes.
Similar Shapes Questions about the scale factors of lengths, areas and volumes of similar shapes. Negative Enlargement A video from MathsWatch about Enlargement by a Negative Scale Factor.
Negative Enlargement A video from MathsWatch about Enlargement by a Negative Scale Factor. Blow Up Click on all the points that could be the centre of enlargement of the shape if the image does not go off the grid.
Blow Up Click on all the points that could be the centre of enlargement of the shape if the image does not go off the grid.
Here are some exam-style questions on this statement:
- "The following points have been plotted then joined up in order to make an irregular hexagon." ... more
- "Describe fully the single transformation that maps trapezium A onto trapezium B." ... more
- "Shape ABCD is a trapezium. It is an enlargement of the smaller blue trapezium with a negative scale factor, \(k\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Enlargements When areas and volumes are enlarged the results are far from intuitive. Doubling the dimensions of a rectangle produces a similar shape with four times the area! Doubling the dimensions of a cuboid produces a similar shape with eight times the volume! The activities provided are intended to give pupils experiences of dealing with enlargements so that they better understand the concept and are able to produce diagrams, make models and answer questions on this subject. Once positive integer scale factors have been mastered the notion of fractional and negative scale factors await discovery!
- Transformations A transformation in mathematics is an operation performed on a shape (or points) which changes the view of that shape (or points). This topic includes four transformations namely reflection, translation, rotations and enlargement. A reflection can best be described as the mirror image of a shape in a given line (which acts as the mirror). After reflection the shape remains the same size but the orientation is the mirror image of the original. The transformation known as a translation can be thought of as a movement or shift in position. The size and orientation of the shape remains the same but the position on the plane changes. A rotation can be described as turning. This transformation is defined by the angle of turning and the centre of rotation (the point which does not move during the turning). Finally enlargement is the term we use when a shape increases in size but maintains the same shape. The shape after enlargement is defines as being similar to the shape before enlargement. His use of the word similar has a precise mathematical meaning. All of the angles in the enlarged shape are the same as the angles in the original shape and the lengths of the sides are in the same proportion. An enlargement is defines by the scale factor of the enlargement and the centre of enlargement. We use the term enlargement even if the shape becomes smaller (a scale factor between minus one and one). A negative scale factor will produce an enlarged mirror image of the original shape.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

