Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
Pascal's Triangle Get to know this famous number pattern with some revealing learning activities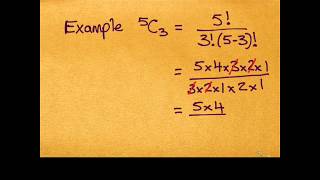
Binomial Theorem Video You may have learnt about the binomial expansion in class some time ago so here's a reminder to bring you up to speed.
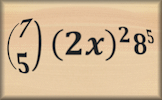Binomial Theorem Exercises in the process of expanding powers of binomial expressions and finding specific coefficients.
Here are some exam-style questions on this statement:
- "If \((x+5)^{10}\) is expanded" ... more
- "If \((2x+7)^{6}\) is expanded" ... more
- "Consider the expansion of:" ... more
- "If you expanded \((2x-3)^{15}\), the term containing \(x^6\) can be written as \(\binom{15}{a}\times(2x)^b\times(-3)^c\)" ... more
- "In the expansion of \( (x+j)^{9}\) where \(j \in \mathbb{R}\), the coefficient of the term in \(x^7\) is 144." ... more
- "The expansion of \((x + g)^7\), where \(g \in \mathbb{Q}^+\), can be written as:" ... more
- "The constant term in the expansion of \(x^4(2x^2+\frac{m}{x})^7\) is 896" ... more
- "Consider the expansion of \( (3x+ \frac{c}{x})^8\) where \( c \gt 0 \). " ... more
- "(a) Find the binomial expansion of \( (1-6x)^{\frac34} \) up to and including the term in \(x^2\)." ... more
- "Consider the expansion of \( (7-x^2)^{n-1}\) where \(n \in \mathbb{Z}^+\). " ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Algebra Pupils begin their study of algebra by investigating number patterns. Later they construct and express in symbolic form and use simple formulae involving one or many operations. They use brackets, indices and other constructs to apply algebra to real word problems. This leads to using algebra as an invaluable tool for solving problems, modelling situations and investigating ideas. If this topic were split into four sub topics they might be: Creating and simplifying expressions; Expanding and factorising expressions; Substituting and using formulae; Solving equations and real life problems; This is a powerful topic and has strong links to other branches of mathematics such as number, geometry and statistics. See also "Number Patterns", "Negative Numbers" and "Simultaneous Equations".
- Combinations "A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange." - Wikipedia In Primary school pupils should practise sorting and grouping items noting similarities and differences. They should develop strategies for finding all the ways a small number of items can be arranged so that missing or duplicates can be found quickly. By the end of Secondary school pupils will have learnt the formulas for combinations and permutations and apply them when solving probability problems.
- Sequences A pattern of numbers following a rule is called a sequence. There are many different types of sequence and this topic introduces pupils to some of them. The most basic sequences of numbers is formed by adding a constant to a term to get the next term of the sequence. This rule can be expressed as a linear equation and the terms of the sequence when plotted as a series of coordinates forms a straight line. More complex sequences are investigated where the rule is not a linear function. Other well-known sequences includes the Fibonacci sequence where the rule for obtaining the next term depends on the previous two terms. Sequences can be derived from shapes and patterns. A growing patterns of squares or triangles formed from toothpicks is often used to show linear sequences in a very practical way. Diagrams representing sequences provides interesting display material for the classroom. Typically pupils are challenged to find the next term of a given sequence but a deeper understanding is needed to find intermediate terms, 100th term or the nth term of a sequence.
Furthermore
Example
To expand \( (2x + 3y)^5 \) using the binomial theorem, we can use the formula:
$$ (a + b)^n = a^n + nC_1 a^{n-1}b + \ldots + nC_r a^{n-r}b^r + \ldots + b^n $$Substituting \( a = 2x \), \( b = 3y \), and \( n = 5 \) into the formula, we get:
$$ (2x + 3y)^5 = (2x)^5 + 5C_1 (2x)^4(3y) + 5C_2 (2x)^3(3y)^2 + 5C_3 (2x)^2(3y)^3 + 5C_4 (2x)(3y)^4 + (3y)^5 $$Simplifying further:
$$ (2x + 3y)^5 = 32x^5 + 160x^4 \cdot 3y + 80x^3 \cdot 9y^2 + 40x^2 \cdot 27y^3 + 10x \cdot 81y^4 + 243y^5 $$Which results in:
$$ (2x + 3y)^5 = 32x^5 + 480x^4y + 720x^3y^2 + 1080x^2y^3 + 810xy^4 + 243y^5 $$This video on the Binomial Theorem is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
