Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Area and Perimeter of a Rectangle Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
Area and Perimeter of a Rectangle Questions on the areas and perimeters of rectangles which will test your problem solving abilities. Area and Perimeter of a Parallelogram Many different ways to practise your skills finding the areas and perimeters of parallelograms.
Area and Perimeter of a Parallelogram Many different ways to practise your skills finding the areas and perimeters of parallelograms. Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.
Area And Perimeter Video Calculate and solve problems involving perimeter and area of rectangles, triangles, parallelograms, trapezia, kites and composite shapes.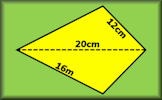 Area and Perimeter of a Kite A short exercise to practise using the formulae for area and perimeter of a kite.
Area and Perimeter of a Kite A short exercise to practise using the formulae for area and perimeter of a kite.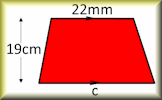 Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
Area of a Trapezium Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.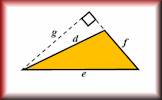 Area and Perimeter Show that you know the area and perimeter formulas of basic shapes.
Area and Perimeter Show that you know the area and perimeter formulas of basic shapes.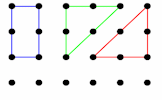 Area Two How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?
Area Two How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?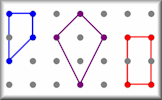 Quad Areas Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
Quad Areas Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid. Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes. Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.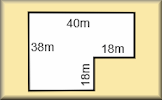 Areas of Composite Shapes Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.
Areas of Composite Shapes Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.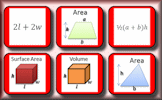 Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes.
Formulae Pairs Find the matching pairs of diagrams and formulae for basic geometrical shapes.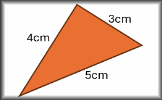 Heron's Formula Use the lengths of the three sides of a triangle to calculate the area.
Heron's Formula Use the lengths of the three sides of a triangle to calculate the area. Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.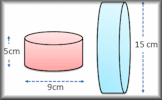 Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Here are some exam-style questions on this statement:
- "A bricklayer estimates the number of bricks he will need to build a wall by dividing the area of the wall by the area of the face of a brick." ... more
- "The diagram shows a water tank in the shape of a cylinder. It has a diameter of 76cm anf a height of 36cm." ... more
- "Babatunde has to paint four containers." ... more
- "The diagram shows a red square placed on top of a grey square." ... more
- "The trapezium and rectangle shown here have the same perimeters. The diagrams are not drawn to scale and the measurements are in centimetres. Calculate the area of the trapezium." ... more
- "The diagram below shows two rectangles not drawn to scale." ... more
- "A container is in the shape of a cuboid as shown in the diagram below." ... more
- "The illustration shows a greenhouse in the shape of a pentagonal prism. The front of the greenhouse is a pentagon with a single line of symmetry. The sides of the greenhouse are vertical." ... more
- "Triangle JKL is the cross-section of a prism of length 25cm." ... more
- "Walter Wall is planning to renovate a remote building by installing new flooring. A diagram showing the area required to be covered by the flooring can be seen below." ... more
- "A red square has sides of length \(x\) cm. A blue rectangle has sides of length \(3x-1\) cm and \(x-2\) cm. The diagrams below are not drawn to scale." ... more
- "A square has sides of length \(x\) cm." ... more
- "The diagram shows a water tank in the shape of a trapezoidal prism." ... more
- "A wedge is to be cut from a log in the shape of a cylinder as shown in the diagram below (not to scale)." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Area Pupils should not only be able to remember and apply area formulae but they should also have a good understanding of what area means. This can be achieved by beginning the study of area with plenty of practical examples. The Pin Board provides an open-ended interactive experimental environment to secure a good fundamental understanding of area. Some examinations provide formulae sheets but it is still important that pupils know the common formulas for finding the areas of basic shapes. They should use these formulae in context to find areas of basic and compound shapes and be able to give answers using appropriate units. Pupils will also learn to find the surface areas of three dimensional shapes, use scale to determine areas from maps and solve real world problems involving areas. See also the topics called Measures, Shape (3D) and Ratio.
- Circles This is all to do with pi and why it is such an important number. From finding the circumference and area of circles to problem solving and investigation. Pupils will begin by learning the names of the parts of a circle then, either through investigation or practical activity, discover that the circumference of a circle is always just a little more than three times the length of the diameter whatever the size of the circle. A brief walk through history leads them to find out how to use this knowledge (and a more accurate version of pi) to find the circumference and areas of circles. This can then be developed to find the area of a sector, area of a segment, area of an annulus and the area of the region between a circle and a square in more complex problem solving situations. More mathematics related to the circle can involve angle theorems, loci and algebra.
- Mensuration Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume. It is linked closely to the topic of Estimation and related to the topics of Angles, Shape and Shave (3D). It is essential for pupils to have an understanding of the units used to measure which include both the more common metric units and the Imperial units still in common usage. We have found a good teaching strategy is to ask each of the pupils to "Bring to the next Maths lesson some visual aid which will help the rest of the class remember the size of a unit of measurement". See Memorable Measures below for the printable resources. This activity provides an association with a unit, a visual aid and a known person which is a great memory enhancer.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

