Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run.
Gradient of a Line Practise the skill of finding the gradients of straight lines by counting squares and dividing rise by run. Straight Line Graphs Video After drawing a straight line graph learn about its equation in the form y = mx + c.
Straight Line Graphs Video After drawing a straight line graph learn about its equation in the form y = mx + c. Straight Line Graph Equation An online exercise about the equation y=mx+c and the features of a straight line graph.
Straight Line Graph Equation An online exercise about the equation y=mx+c and the features of a straight line graph. Don's Graph Snaps Complete the tables and find the equations of the graphs that can be seen in the snaps.
Don's Graph Snaps Complete the tables and find the equations of the graphs that can be seen in the snaps. Graph Patterns Find the equations which will produce the given patterns of graphs.
Graph Patterns Find the equations which will produce the given patterns of graphs. Line Graph Challenge A challenge to produce the straight line patterns using a GDC or graph plotting software.
Line Graph Challenge A challenge to produce the straight line patterns using a GDC or graph plotting software. Straight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator.
Straight Line Graphs 10 straight line graph challenges for use with computer graph plotting software or a graphical display calculator. Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.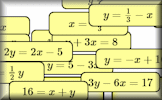 Parallel Graphs Collect together in groups the equations of the graphs that are parallel to each other.
Parallel Graphs Collect together in groups the equations of the graphs that are parallel to each other. Perpendicular Pairs Find the pairs of equations that will produce perpendicular graphs.
Perpendicular Pairs Find the pairs of equations that will produce perpendicular graphs. Equation of Line through Points Video A short video showing how to find the equation of a line that passes through given points.
Equation of Line through Points Video A short video showing how to find the equation of a line that passes through given points. Equation of a Line Through Points Match the equations of the straight line graphs to the clues about gradients and points.
Equation of a Line Through Points Match the equations of the straight line graphs to the clues about gradients and points. Coordinate Geometry Table Fill in the empty cells of this table with information about lines, gradients and coordinates.
Coordinate Geometry Table Fill in the empty cells of this table with information about lines, gradients and coordinates.
Here are some exam-style questions on this statement:
- "The equation of the line L1 is \(y = 2 - 5x\)." ... more
- "Which of the following lines is parallel to the x-axis?" ... more
- "Show that line \(5y = 7x - 7\) is perpendicular to line \(7y = -5x + 55\)." ... more
- "A straight line goes through the points \((a, b)\) and \((c, d)\), where" ... more
- "The straight line \(L\) has the equation \(4y = 3x + 5\)." ... more
- "Suppose a rhombus ABCD is drawn on a coordinate plane with the point A situated at (4,7). The diagonal BD lies on the line \(y = 2x - 5 \)" ... more
- "Consider the points A(-5, 15). B(4, 6) and C(-8, 12). The line \(L\) passes through the point A and is perpendicular to [BC]." ... more
Here are some Advanced Starters on this statement:
- Parallel Graphs
Determine from their equations which of the straight line graphs are parallel and perpendicular. more - Venn Graphs
Type the equation of a graph into each section of the Venn diagram. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
The equation of a straight line can be expressed in various forms, each highlighting different aspects of the line's geometric properties. The most common forms are:
1. Slope-Intercept Form: \( y = mx + c \), where \( m \) is the gradient (slope) and \( c \) is the y-intercept. This form is useful for easily identifying the slope and y-intercept of the line.
$$ y = mx + c $$
Example: The line with gradient 3 and y-intercept -2 is given by \( y = 3x - 2 \).
2. Point-Slope Form: \( y - y_1 = m(x - x_1) \), where \( (x_1, y_1) \) is a point on the line and \( m \) is the gradient. This form is helpful when a point on the line and the slope are known.
$$ y - y_1 = m(x - x_1) $$
Example: A line passing through the point (2, 3) with a gradient of 4 is given by \( y - 3 = 4(x - 2) \).
3. General Form: \( Ax + By + C = 0 \), where A, B, and C are constants. This form is useful for certain algebraic manipulations and geometric interpretations.
$$ Ax + By + C = 0 $$
Example: The line with equation \( 2x + 3y - 6 = 0 \) can be rearranged to slope-intercept form as \( y = -\frac{2}{3}x + 2 \).
For parallel and perpendicular lines:
Parallel Lines: Two lines are parallel if they have the same gradient. For lines \( y = m_1x + c_1 \) and \( y = m_2x + c_2 \), they are parallel if \( m_1 = m_2 \).
Perpendicular Lines: Two lines are perpendicular if the product of their gradients is -1. For lines \( y = m_1x + c_1 \) and \( y = m_2x + c_2 \), they are perpendicular if \( m_1 \times m_2 = -1 \).
$$ \text{For parallel lines: } m_1 = m_2 $$ $$ \text{For perpendicular lines: } m_1 \times m_2 = -1 $$
This video on Forms of Linear Lines is from Revision Village and is aimed at students taking the IB Maths AI Standard level course
This video on Gradients and Intercepts of Linear Lines is from Revision Village and is aimed at students taking the IB Maths AI Standard level course.
This video on Parallel and Perpendicular Gradients is from Revision Village and is aimed at students taking the IB Maths Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

