International Baccalaureate Mathematics

Syllabus Content

Derivative of xⁿ, sinx, cosx, e^x and lnx. Differentiation of a sum and a multiple of these functions. The chain rule for composite functions. The product and quotient rules

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

Differentiation Video A reminder of how to differentiate different types of functions and how to find the equations of tangents and normals.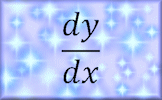

Differentiation Practise the technique of differentiating polynomials with this self marking exercise.

Here are some exam-style questions on this statement:

"A function is given as $f(x)=3x^2-6x+4+\frac3x,-2\le x \le 4, x\ne 0$." ... more

"Consider the graph of the function $f(x)=7-3x^2-x^3$" ... more

"Consider the graph of $f(x)=a\sin(b(x+c))+12$, for $0\le x\le 24$." ... more

"(a) Find $ \frac{dy}{dx} $ when:" ... more

"Consider the function $f$ defined by $f(x)= \ln{(x^2 - 9)}$ for $x > 3$." ... more

"The diagram shows part of the graph of $y=a\sin{(bx)}+c$ with a minimum at $(-2.5,-2)$ and a maximum at $(2.5,4)$." ... more

"The function $f$ is defined by $f(x) = 8 - 5 \sin{x} $, for $ x \ge 0 $." ... more

"A particle moves in a straight line such that its velocity, $v$ ms^-1, at time $t$ seconds is given by:" ... more

"Consider the cubic function $f(x)=\frac{1}{6}x^3-2x^2+6x-2$" ... more

"Consider the function $f(x)=x^3-9x+2$." ... more

"The displacement, in millimetres, of a particle from an origin, O, at time t seconds, is given by $s(t) = t^3 cos t + 5t sin t$ where $ 0 \le t \le 5 $ ." ... more

"The function $f$ is defined as follows:" ... more

"Consider the functions" ... more

"A particle P moves along a straight line. The velocity $v$ in metres per second of P after $t$ seconds is given by $v(t) = 3\sin{t} - 8t^{\cos{t}}, 0 \le t \le 7$." ... more

"Consider a function $f$, such that $f(x)=7.2\sin(\frac{\pi}{6}x + 2) + b$ where $ 0\le x \le 12$" ... more

"Consider the function $f$ defined by $f(x) = 25e^{x-5}$ for $x \in \mathbb{R}^+$." ... more

"The height of water in metres above Chart Datum* in the Port of Bristol on a day in January is modelled by the function:" ... more

"Let $f(x) = \frac{ln3x}{kx} $ where $ x \gt 0$ and $ k \in \mathbf Q^+ $." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Calculus It is said that the word calculus comes from the Latin word for the small pebble used for counting and calculations. The two major branches, differentiation and integration, are studied by pupils only towards the end of their school days but does then form a major part of their studies. A course in calculus is a prerequisite for other, more advanced courses in mathematical analysis. Isaac Newton is best known for developing calculus. He was born in England in 1642 and is considered one of the most influential scientists and mathematicians in history.

Furthermore

Official Guidance, clarification and syllabus links:

Examples: $f(x)=e^{(x^2+2)}, \quad f(x)=\sin(3x-1) $

Link to: composite functions (SL2.5).

Formula Booklet:

Derivative of $\sin{x}$	$ f(x)= \sin x \quad \Rightarrow \quad f'(x) = \cos x $
Derivative of $\cos{x} $	$ f(x)= \cos x \quad \Rightarrow \quad f'(x) = i\sin x $
Derivative of $e^x$	$ f(x)= e^x \quad \Rightarrow \quad f'(x) = e^x $
Derivative of $\ln x$	$ f(x)= \ln x \quad \Rightarrow \quad f'(x) = \dfrac{1}{x} $
Chain rule	$ y=g(u), \text{ where } u = f(x) \Rightarrow \quad \dfrac{dy}{dx} = \dfrac{dy}{du} \times \dfrac{du}{dx} $
Product rule	$ y=uv \quad \Rightarrow \quad \dfrac{dy}{dx} = u\dfrac{dv}{dx} + v\dfrac{du}{dx} $
Quotient rule	$ y=\dfrac{u}{v} \quad \Rightarrow \quad \dfrac{dy}{dx} = \dfrac{v \frac{du}{dx} - u \frac{dv}{dx}}{v^2} $

Examples

1. Chain Rule:
The chain rule is used when differentiating composite functions. If we have a function $ y = f(u) $ and $ u = g(x) $, then the derivative of $ y $ with respect to $ x $ is given by:

$$ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} $$

Example: Differentiate $ y = \sin(3x^2) $ with respect to $ x $.

Let $ u = 3x^2 $. Then, $ \frac{du}{dx} = 6x $ and $ \frac{dy}{du} = \cos(u) $. Using the chain rule:

$$ \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

2. Product Rule:
The product rule is used when differentiating the product of two functions. If $ y = u \cdot v $ where both $ u $ and $ v $ are functions of $ x $, then the derivative of $ y $ with respect to $ x $ is:

$$ \frac{dy}{dx} = u' \cdot v + u \cdot v' $$

Example: Differentiate $ y = x^2 \cdot \ln(x) $ with respect to $ x $.

Using the product rule:

$$ \frac{dy}{dx} = 2x \cdot \ln(x) + x^2 \cdot \frac{1}{x} = 2x \ln(x) + x $$

3. Quotient Rule:
The quotient rule is used when differentiating the quotient of two functions. If $ y = \frac{u}{v} $ where both $ u $ and $ v $ are functions of $ x $ and $ v \neq 0 $, then the derivative of $ y $ with respect to $ x $ is:

$$ \frac{dy}{dx} = \frac{u' \cdot v - u \cdot v'}{v^2} $$

Example: Differentiate $ y = \frac{x^2}{\sin(x)} $ with respect to $ x $.

Using the quotient rule:

$$ \frac{dy}{dx} = \frac{2x \cdot \sin(x) - x^2 \cdot \cos(x)}{\sin^2(x)} $$

This video on the Basics of Differentiation is from Revision Village and is aimed at students taking the IB Maths Standard level course

Here's a 'deep fake' video featuring the images of Arnold Schwarzenegger, Ice Spice and Mr Beast explaining the chain rule for differentiation. While the humans might be fake the maths is real and correct.

If you use a TI-Nspire GDC there are instructions useful for this topic.

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

Derivative of \(\sin{x}\)	\( f(x)= \sin x \quad \Rightarrow \quad f'(x) = \cos x \)
Derivative of \(\cos{x} \)	\( f(x)= \cos x \quad \Rightarrow \quad f'(x) = i\sin x \)
Derivative of \(e^x\)	\( f(x)= e^x \quad \Rightarrow \quad f'(x) = e^x \)
Derivative of \(\ln x\)	\( f(x)= \ln x \quad \Rightarrow \quad f'(x) = \dfrac{1}{x} \)
Chain rule	\( y=g(u), \text{ where } u = f(x) \Rightarrow \quad \dfrac{dy}{dx} = \dfrac{dy}{du} \times \dfrac{du}{dx} \)
Product rule	\( y=uv \quad \Rightarrow \quad \dfrac{dy}{dx} = u\dfrac{dv}{dx} + v\dfrac{du}{dx} \)
Quotient rule	\( y=\dfrac{u}{v} \quad \Rightarrow \quad \dfrac{dy}{dx} = \dfrac{v \frac{du}{dx} - u \frac{dv}{dx}}{v^2} \)