Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
Maxvoltray Find the maximum volume of a tray made from an A4 sheet of paper. A practical mathematical investigation.
Differentiation Video A reminder of how to differentiate different types of functions and how to find the equations of tangents and normals.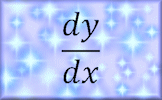
Differentiation Practise the technique of differentiating polynomials with this self marking exercise.
Here are some exam-style questions on this statement:
- "A function is given as \(f(x)=3x^2-6x+4+\frac3x,-2\le x \le 4, x\ne 0\)." ... more
- "Consider the graph of the function \(f(x)=7-3x^2-x^3\)" ... more
- "A child's play tent is made in the shape of half a cylinder. It is constructed from a fibreglass frame with material pulled tightly around it. The fibreglass frame consists of a rectangular base, two semi-circular ends and two further support rods, as shown in the following diagram." ... more
- "A package is in the shape of a cuboid and has a length \(l\) cm, width \(w\) cm and height of 12 cm." ... more
- "Consider the cubic function \(f(x)=\frac{1}{6}x^3-2x^2+6x-2\)" ... more
- "The displacement, in millimetres, of a particle from an origin, O, at time t seconds, is given by \(s(t) = t^3 cos t + 5t sin t\) where \( 0 \le t \le 5 \) ." ... more
- "A circle with equation \(x^2+y^2=25 \) has centre \((0,0)\) and radius 5." ... more
- "The following diagram shows part of the graph of \(y=f (x)\)" ... more
- "Moresum Soup is sold in cans with a capacities of 400ml each. Each can is in the shape of a right circular cylinder with radius \(r\) cm and height \(h\) cm." ... more
- "The following diagram shows the graph of \(f'\), the first derivative of a function \(f\)." ... more
- "Let \(f(x) = \frac{ln3x}{kx} \) where \( x \gt 0\) and \( k \in \mathbf Q^+ \)." ... more
Here are some Advanced Starters on this statement:
- Fence Optimisation
Find the length of a rectangle enclosing the largest possible area. more - Road Connections
Design roads to connect four houses that are on the corners of a square, side of length one mile, to minimise the total length of the roads. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
This Optimisation video is from Revision Village and is aimed at students taking the IB Maths Standard level course.
A local maximum is a point where a function has a higher value than at nearby points, making it a peak in the graph. Conversely, a local minimum is a point where the function has a lower value than its neighbours, forming a trough. To test for these points, we often use the first and second derivative tests. If \( f'(x) \) changes sign from positive to negative as \( x \) increases, \( f(x) \) has a local maximum. If \( f'(x) \) changes from negative to positive, \( f(x) \) has a local minimum. The second derivative test states that if \( f''(x) > 0 \) at a point where \( f'(x) = 0 \), then \( f(x) \) has a local minimum. If \( f''(x) < 0 \), it's a local maximum.
Optimisation involves finding the maximum or minimum values of a function in a given domain, which has numerous applications in real-world scenarios, such as maximising profit or minimising cost.
A point of inflexion is where a curve changes its curvature direction. If the curve changes from concave upwards to concave downwards (or vice versa), it's an inflexion point. At these points, \( f''(x) = 0 \) or is undefined. However, not all points where \( f''(x) = 0 \) are inflexion points. The gradient at an inflexion point can be zero (a horizontal tangent) or non-zero.
Examples:
1) Consider the function \( f(x) = x^3 - 3x^2 \).
The first derivative is \( f'(x) = 3x^2 - 6x \) and the second derivative is \( f''(x) = 6x - 6 \).
Setting \( f'(x) = 0 \), we get \( x = 0 \) and \( x = 2 \). Using the second derivative test, we find that \( f(x) \) has a local maximum at \( x = 0 \) and a local minimum at \( x = 2 \).
2) For the function \( g(x) = x^4 - 4x^3 \),
The first derivative is \( g'(x) = 4x^3 - 12x^2 \) and the second derivative is \( g''(x) = 12x^2 - 24x \).
Setting \( g''(x) = 0 \), we get \( x = 0 \) and \( x = 2 \). Both of these are points of inflexion, but only \( x = 2 \) has a gradient of zero.
A stationary point has a gradient of zero.
A turning point is a minimum or maximum.
A point of inflection is where the second derivative is zero
This video on Optimization and Calculus Curves is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course.
Transum,
Saturday, August 17, 2019
"My favourite optimisation problem is the farmer's dilemma. It's one of the Advanced Starters and can be found here
"
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.
