International Baccalaureate Mathematics

Syllabus Content

Definite integrals, including analytical approach. Areas of a region enclosed by a curve y=f(x) and the x-axis, where f(x) can be positive or negative, without the use of technology. Areas between curves

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

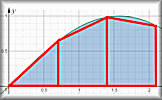Trapezium Rule Practise using the trapezium rule to find an approximate value for the area under a curve.

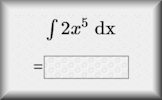Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.

Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.

Here are some exam-style questions on this statement:

"The graph of $f(x)=8-x^2$ crosses the x-axis at the points A and B." ... more

"The acceleration, $a$ ms^-2 , of an object at time $t$ seconds is given by" ... more

"Find:" ... more

"The diagram below shows part of the graph of $y = \dfrac{2x}{9-x^2}$" ... more

"Consider the region where $0 \lt x \lt 2\pi $ and $\sin{x} \gt \cos{2x} $" ... more

"The function $f$ is defined by $f(x) = 8 - 5 \sin{x} $, for $ x \ge 0 $." ... more

"A particle moves in a straight line such that its velocity, $v$ ms^-1, at time $t$ seconds is given by:" ... more

"(a) Use the trapezium rule with 4 ordinates to estimate to 2 decimal places the value of" ... more

"Consider the graph of the function $f(x)=x^2+2$." ... more

"(a) Express the algebraic fraction" ... more

"Make a sketch of a graph showing the velocity (in $ms^{-1}$) against time of a particle travelling for six seconds according to the equation:" ... more

"Find the value of $a$ if $\pi \lt a \lt 2\pi$ and:" ... more

"This graph represents the function $f:x\to a \cos x, a\in \mathbf N$" ... more

"Consider the function $f$ defined by $f(x) = 25e^{x-5}$ for $x \in \mathbb{R}^+$." ... more

"The following diagram shows the graph of $f(x) = \cos(e^x) \; \text{for} \; 0 \le x \le 0.5$." ... more

"Let $f(x) = \frac{ln3x}{kx} $ where $ x \gt 0$ and $ k \in \mathbf Q^+ $." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Calculus It is said that the word calculus comes from the Latin word for the small pebble used for counting and calculations. The two major branches, differentiation and integration, are studied by pupils only towards the end of their school days but does then form a major part of their studies. A course in calculus is a prerequisite for other, more advanced courses in mathematical analysis. Isaac Newton is best known for developing calculus. He was born in England in 1642 and is considered one of the most influential scientists and mathematicians in history.

Furthermore

Official Guidance, clarification and syllabus links: $$\int_{a}^{b} g'(x) \; dx = g(b)-g(a)$$

The value of some definite integrals can only be found using technology.

Link to: definite integrals using technology

Students are expected to first write a correct expression before calculating the area.

Technology may be used to enhance understanding of the relationship between integrals and areas.

Formula Booklet:

Area of region enclosed by a curve and x-axis

$$A = \int_{a}^{b} |y| \; dx $$

Areas between curves

We want to find the area between the curves $ y = x^2 + x - 2 $ and $ y = x + 2 $. First, we need to find the points of intersection between the two curves.

We can do this by setting the two equations equal to each other and solving for $ x $:

\[ \begin{align*} x^2 + x - 2 &= x + 2 \\ x^2 &= 4 \\ (x - 2)(x + 2) &= 0. \end{align*} \]

The solutions are $ x = 2 $ and $ x = -2 $, so the curves intersect at these points.

Next, we'll find the area between the curves by integrating the difference between the two functions over the interval from $-2$ to $2$

\[ \begin{align*} \text{Area} &= \int_{-2}^{2} \left( x + 2 - (x^2 + x - 2) \right) \,dx \\ &= \int_{-2}^{2} \left( -x^2 + 4 \right) \,dx \\ &= \left[ - \frac{x^3}{3} + 4x \right]_{-2}^2\\ &=(-8/3+8)-(8/3-8)\\ &=10 \frac23 \text{ square units} \end{align*} \]

This Finding Areas Under Curves video is from Revision Village and is aimed at students taking the IB Maths Standard level course

Trapezium Rule is a textbook style page with a few worked examples from Alevelmaths.co.uk.

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.