International Baccalaureate Mathematics

Syllabus Content

Counting principles, including permutations and combinations. Extension of the binomial theorem to fractional and negative indices, ie (a+b)ⁿ, n ∈ Q

Here are some exam-style questions on this statement:

"Consider the expansion of:" ... more

"Nine cats squeeze through a gap in a fence to get to a fish pond. There is only enough room for one cat at a time to squeeze through the gap." ... more

"A fund-raising activity involves people choosing three balls from a jar containing balls numbered 1 to 30. A prize of £5 is awarded if the three numbers chosen sum to a multiple of three. It costs £2 to have a go." ... more

"Fifty years ago there was a zoo where animals were housed in cages. There were eight animal cages in a line on the northern perimeter of the zoo. Only four cages were being used: one to hold the gorilla, one for the chimpanzees, one for the gibbons and one for the macaques." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Combinations "A combination is a way of selecting several things out of a larger group, where (unlike permutations) order does not matter. In smaller cases it is possible to count the number of combinations. For example given three fruit, say an apple, orange and pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange." - Wikipedia In Primary school pupils should practise sorting and grouping items noting similarities and differences. They should develop strategies for finding all the ways a small number of items can be arranged so that missing or duplicates can be found quickly. By the end of Secondary school pupils will have learnt the formulas for combinations and permutations and apply them when solving probability problems.

Furthermore

Official Guidance, clarification and syllabus links:

Not required:

Permutations where some objects are identical.

Circular arrangements.

Formula Booklet: AHL 1.10

Combinations	$ ^nC_r = \dfrac{n!}{r!(n-r)!} $
Permutations	$ ^nP_r = \dfrac{n!}{(n-r)!} $

The product principle states that if there are $n$ different ways of performing an action, and for each of these there are $p$ different ways of performing a second independent action, then there are $np$ different ways of performing the two operations in succession.

The sum principle is a counting rule that tells us how many ways we can perform an action. If we have $n$ different ways of performing an action OR $p$ different ways of performing a different, mutually exclusive action, then the sum principle tells us that there are a total of $n+p$ different ways we can perform the action.

For example:

How many ways are there of getting from A to D?

How many ways are there of getting from C to D?

How many ways are there of getting from B to D?

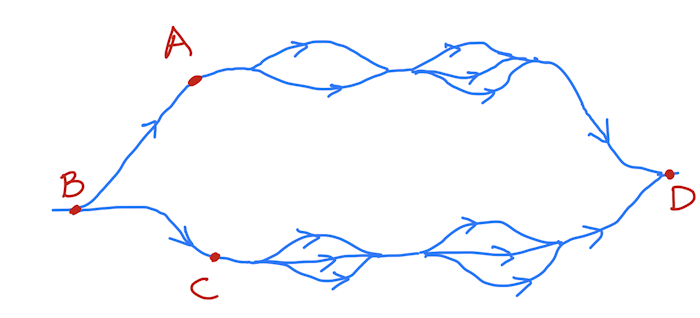
There are $2 \times 3 = 6$ ways of getting from A to D (product principle).

There are $3 \times 3 = 9$ ways of getting from C to D (product principle).

There are $6 + 9 = 15$ ways of getting from B to D (sum principle).

Counting principles, including permutations and combinations, are fundamental concepts in combinatorics that are used to count the number of ways to choose or arrange objects in a set. Permutations and combinations are different ways of counting and are often used in probability problems.

Permutations:

$$\large{_{n}P_{r} = \frac{n!}{(n-r)!}}$$

Where n is the number of objects in a set and r is the number of objects chosen. This formula calculates the number of ordered arrangements of r objects chosen from a set of n objects.

For example, suppose we have a set of 5 different letters: A, B, C, D, E. How many ways are there to arrange 3 of these letters?

We can use the permutation formula:

$$\large{_{5}P_{3} = \frac{5!}{(5-3)!} = \frac{5\times4\times3\times2\times1}{2\times1} = 60}$$

Therefore, there are 60 different ways to arrange 3 letters from a set of 5 letters.

Combinations:

$$\large{{n \choose r} = \frac{n!}{r!(n-r)!}}$$

Where n is the number of objects in a set and r is the number of objects chosen. This formula calculates the number of ways to choose r objects from a set of n objects, without regard to order.

For example, suppose we have a set of 5 different letters: A, B, C, D, E. How many ways are there to choose 3 of these letters?

We can use the combination formula:

$$\large{{5 \choose 3} = \frac{5!}{3!(5-3)!} = \frac{5\times4\times3\times2\times1}{3\times2\times1\times2\times1} = 10}$$

Therefore, there are 10 different ways to choose 3 letters from a set of 5 letters.

The binomial theorem is a formula that allows us to expand expressions of the form $$(a+b)^n$$ where n is a positive integer. However, it can be extended to allow for fractional and negative indices, which can be useful in certain situations.

Tip worth remembering

To find the binomial expansion of $ (2+x)^{ -\frac12} $ reduce the first term to one by taking out a factor of 2. It then becomes $ 2^{- \frac12} (1+ \frac{x}{2})^{-\frac12} $

Then use the formula:

$$ (a+bx)^{n} = a^{n} \sum_{k=0}^{\infty} {n \choose k} \left(\frac{bx}{a}\right)^k $$

This is the formula to remember as it makes the working as easy as possible.

$$ 2^{-\frac12} \left(1+ \frac{x}{2} \right)^{-\frac12} = \dfrac{1}{\sqrt{2}} \left(1 - \dfrac{x}{4} + \dfrac{3x^2}{32} - \dfrac{5x^3}{128} + \cdots \right) $$

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

Combinations	\( ^nC_r = \dfrac{n!}{r!(n-r)!} \)
Permutations	\( ^nP_r = \dfrac{n!}{(n-r)!} \)

International Baccalaureate Mathematics

Number and Algebra

Furthermore