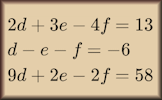International Baccalaureate Mathematics

Syllabus Content

Solutions of systems of linear equations (a maximum of three equations in three unknowns), including cases where there is a unique solution, an infinite number of solutions or no solution.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

Three Unknowns Solve these sets of three simultaneous, linear equations to find the values of the variables.

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Simultaneous Equations This topic covers simultaneous equations with two different variables. The starters pose real world problems which can be solved using the techniques taught at school or by other intuitive methods. Though there are many formal strategies for solving simultaneous equations the skill of forming the equations from real life situations is a very important stage in working towards a solution. Algebraic methods are the most efficient for solving basic simultaneous equations but graphical methods, probably using a graphic display calculator or computer software package, may be more suitable for less standard sets of simultaneous equations.

Furthermore

Official Guidance, clarification and syllabus links:

These systems should be solved using both algebraic and technological methods, for example row reduction or matrices.

Systems which have no solution(s) are inconsistent.

Finding a general solution for a system with an infinite number of solutions.

The augmented matrix can be used to determine the number of solutions:

$$\left[\begin{array}{ccc|c}a & b & c & d\\0 & e & f & g\\0 & 0 & h & i\end{array}\right]$$

If $ h \neq 0$ there is a unique solution.

If $ h = 0 \text{ and } i \neq 0 $ there is no solution

If $ h = 0 \text{ and } i = 0 $ there are infinitely many solutions (let $z=t$).

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

International Baccalaureate Mathematics

Number and Algebra

Furthermore