International Baccalaureate Mathematics

Syllabus Content

Derivatives of tanx, secx, cosecx, cotx, a^x, log_ax, arcsinx, arccosx, arctanx.
Indefinite integrals of the derivatives of any of the above functions.
The composites of any of these with a linear function.
Use of partial fractions to rearrange the integrand.

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

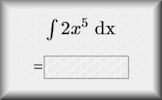Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.

Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.

Partial Fractions Exercises on mastering the art of partial fraction decomposition.

Integration Flowchart This flowchart will only be of use to those who have already learnt the techniques mentioned in the IB AA Syllabus.

Here are some exam-style questions on this statement:

"Consider the functions $f(x)=\sin(x) \text{ and } g(x) = \tan(x+\frac{\pi}{2})$ in the region where $\frac{\pi}{2}\le x \le \pi$" ... more

"The curve $ y=\sin(\sqrt{x}) \text{ where } x \ge 0 $ intersects the x axis at the points $x_0, x_1, x_2, x_3, x_4, ... $ and $x_0 = 0$." ... more

"A function $ f $ is defined by $ f(x) = \arccos\left(\frac{x^2}{1-x^4}\right) $, $ x \in \mathbb{R} $, $ 0.785 \lt |x| \lt 5$." ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Calculus It is said that the word calculus comes from the Latin word for the small pebble used for counting and calculations. The two major branches, differentiation and integration, are studied by pupils only towards the end of their school days but does then form a major part of their studies. A course in calculus is a prerequisite for other, more advanced courses in mathematical analysis.

Furthermore

Official Guidance, clarification and syllabus links:

Indefinite integral interpreted as a family of curves.

$$ \text{Examples } \int \dfrac{1}{x^2+2x+5}dx=\dfrac{1}{2}\arctan{\frac{(x+1)}{2}+C} $$ $$ \int \sec^2{(2x+5)}dx = \dfrac{1}{2} \tan{(2x+5)}+C$$

$$ \int \dfrac{1}{x^2+3x+2}dx = \ln|\frac{x+1}{x+2}| + C $$

Link to: partial fractions (AHL1.11)

Formula Booklet:

Standard derivatives

$ \frac{d}{dx} \tan(x) = \sec^2(x) $

$ \frac{d}{dx} \sec(x) = \sec(x) \tan(x) $

$ \frac{d}{dx} \cosec(x) = -\cosec(x) \cot(x) $

$ \frac{d}{dx} \cot(x) = -\cosec^2(x) $

$ \frac{d}{dx} a^x = a^x \ln(a) $

$ \frac{d}{dx} \log_a(x) = \frac{1}{x \ln(a)} $

$ \frac{d}{dx} \arcsin(x) = \frac{1}{\sqrt{1 - x^2}} $

$ \frac{d}{dx} \arccos(x) = -\frac{1}{\sqrt{1 - x^2}} $

$ \frac{d}{dx} \arctan(x) = \frac{1}{1 + x^2} $

Standard Integrals

$ \int a^x dx = \dfrac{1}{\ln{a}}a^x + C$

$ \int \dfrac{1}{a^2+x^2} dx = \dfrac{1}{a} \arctan{\left(\frac{x}{a}\right)}+C $

$ \int \dfrac{1}{\sqrt{a^2-x^2}} dx = \arcsin{\left(\frac{x}{a}\right)}+C, \quad |x|\lt a $

See the main Partial Fractions section of the syllabus in Number and Algebra.

Here is an example of how to use partial fractions to decompose the rational function $ \dfrac{2x-5}{(x-2)(x+1)^2} $:

$$\begin{aligned} \frac{2x-5}{(x-2)(x+1)^2} &= \frac{A}{x-2} + \frac{B}{x+1} + \frac{C}{(x+1)^2} \\ &= \frac{A(x+1)^2 + B(x-2)(x+1) + C(x-2)}{(x-2)(x+1)^2} \end{aligned} $$

Multiplying both sides by the common denominator gives:

$$2x-5 = A(x+1)^2 + B(x-2)(x+1) + C(x-2)$$

Substituting $x = 2$ gives:

$$-1 = 9A$$ $$A = -\dfrac{1}{9}$$

Substituting $x = -1$ gives:

$$-7 = -3C$$ $$C = \dfrac{7}{3}$$

Finally, substituting $x = 0$ gives:

$$-5 = A - 2B -2C$$

Substituting A and C gives:

$$-5 = \left(-\frac{1}{9}\right) - 2B + -2\left( \frac{7}{3} \right)$$ $$B = \dfrac{1}{9}$$

Therefore, we have:

$$\frac{2x-5}{(x-2)(x+1)^2} = -\frac{1}{9(x-2)} + \frac{1}{9(x+1)} + \frac{7}{3(x+1)^2}$$

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.