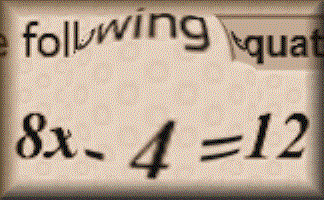There are 366 different Starters of The Day, many to
choose from. You will find below some starters on the topic of Angles. A lesson starter does not have to be on the same
topic as the main part of the lesson or the topic of the previous lesson. It is
often very useful to revise or explore other concepts by using a starter based on a
totally different area of Mathematics.
Main Page
Angles Starters:

Work out which aircraft are in danger of colliding from their positions and direction of travel. An exercise in understanding bearings.
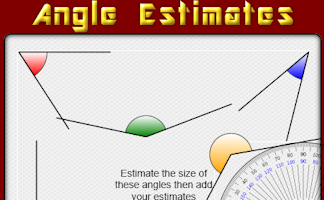
Estimate the sizes of each of the angles then add your estimates together.
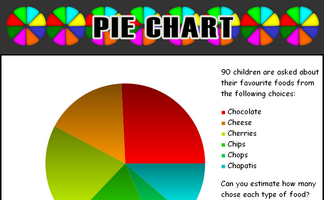
An exercise in estimating what the sectors of a pie chart represent.

Work out which sectors fit together to make complete circles. Knowledge of the sum of the angles at a point will help find more than one correct solution to this puzzle.
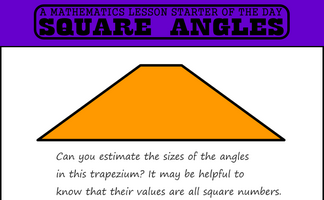
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.
Advanced Angles Starters
Exercises
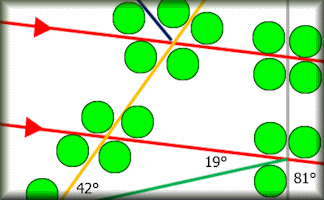
Angle Chase
Find all of the angles on the geometrical diagrams.
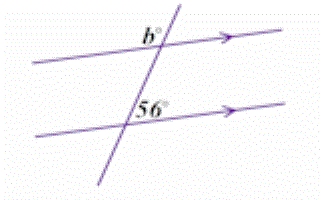
Angle Parallels
Understand and use the relationship between parallel lines and alternate and corresponding angles.
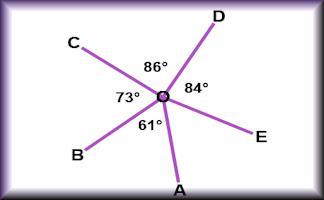
Angle Points
Apply the properties of angles at a point, angles on a straight line and vertically opposite angles.
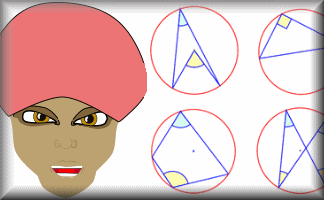
Angle Theorem Kim's Game
A memory game to be projected to help the whole class revise the circle angle theorems.
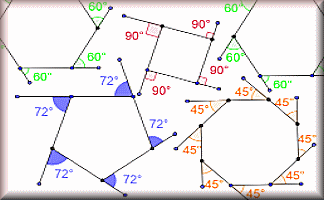
Angle Theorems
Diagrams of the angle theorems with interactive examples.
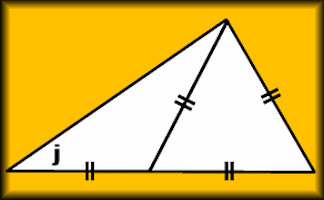
Angles in a Triangle
A self marking exercise involving calculating the unknown angle in a triangle.
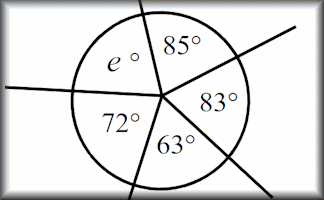
Angles Mixed
Find the unknown angles by using the basic angle theorems.
Circle Theorem Pairs
A pairs game based around ten theorems about the angles made with chords, radii and tangents of circles.
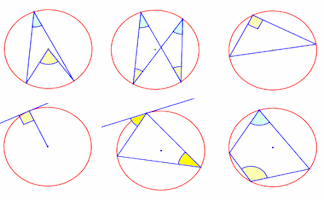
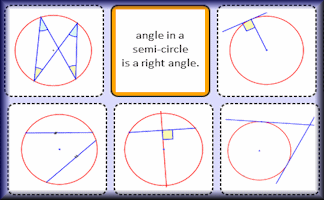
Circle Theorems
Diagrams of the circle theorems to be projected onto a white board as an effective visual aid.
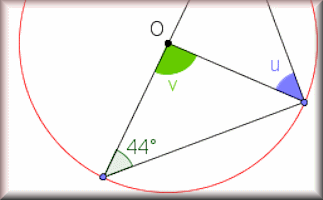
Circle Theorems Exercise
Show that you understand and can apply the circle theorems with this self marking exercise.
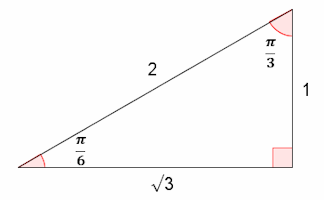
Common Trig Ratios Radians
A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles given in radians.

Estimating Angles
Estimate the size of the given acute angles in degrees.
Geometry Toolbox
Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.

Kite Maths
Can you make a kite shape from a single A4 size sheet of paper using only three folds?
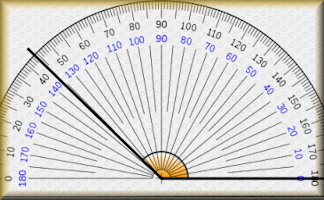
Measuring Angles
Measure the size of the given angles to within two degrees of their actual value.
Online Logo
An online version of the Logo programming language with 30 mathematical challenges.
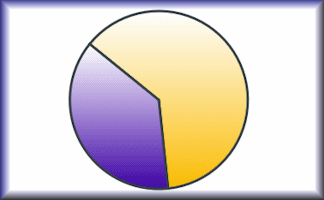
Pie Charts
Develop the skills to construct and interpret pie charts in this self-marking set of exercises.

Plane Bearings
A visual aid designed to help pupils estimate three figure bearings.

Polygon Angle Explorer
Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
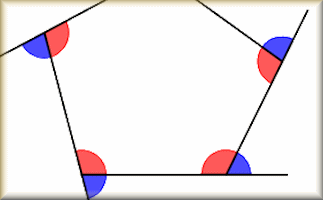
Polygon Angles
A mixture of problems related to calculating the interior and exterior angles of polygons.

Polygon Profiles
A visual aid about the properties of regular polygons designed to be projected onto a whiteboard for whole class exposition.
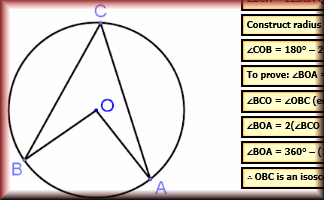
Proof of Circle Theorems
Arrange the stages of the proofs for the standard circle theorems in the correct order.

Scale Drawings
Measure line segments and angles in geometric figures, including interpreting scale drawings.
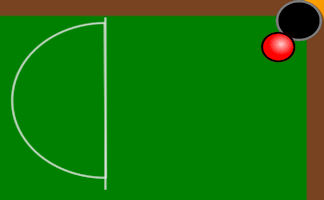
Snooker Angles
An online game for one or two players requiring an ability to estimate angles as bearings.
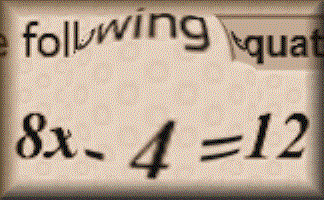
Words and Concepts
Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, angles and shapes.
Other activities for this topic | | |
Complete Index of Starters
Search
The activity you are looking for may have been classified in a different way from the way you were expecting. You can search the whole of Transum Maths by using the box below.
Have today's Starter of the Day as your default homepage. Copy the URL below then select
Tools > Internet Options (Internet Explorer) then paste the URL into the homepage field.
Set as your homepage (if you are using Internet Explorer)
Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world.
Click here to enter your comments.