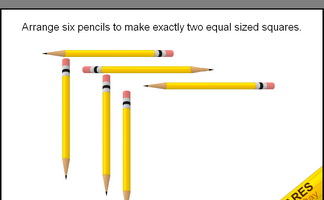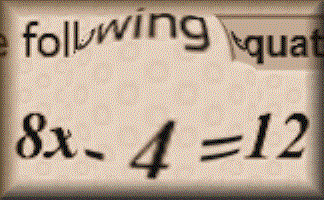Shape Starters:

How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?

Which of the two shapes has the largest area? You will be surprised!
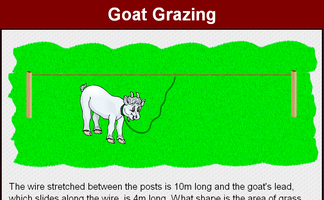
Find the loci of the goat's position as it eats the grass while tethered to the rope.

On a full page in the back of your exercise book draw a perfectly regular hexagon.
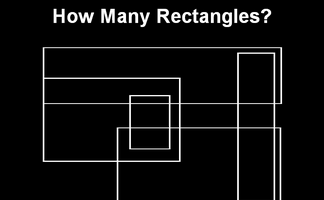
How many rectangles can you find in this pattern? Can you come up with a systematic method for counting them all?

Work out how many squares are there altogether in the given pattern then tackle the chess board.

How many squares can be found by joining four dots on the grid?

How many Triangles can you find in the diagram?

How many triangles are hidden in the pattern? What strategy might you use to count them all to ensure you don't miss any out?
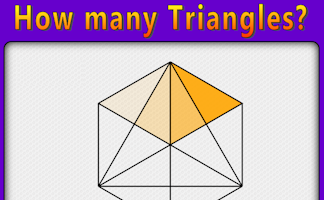
Find a systematic way of counting the number of triangles in the given diagram.
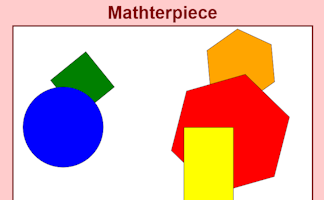
Memorise a picture made up of geometrical shapes

The missing square puzzle is an optical illusion used to help students reason about geometrical figures.

Find the dimensions of a rectangle given the perimeter and area.
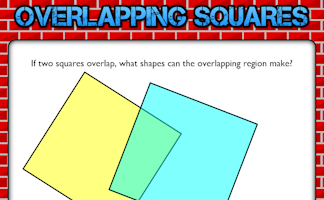
If two squares overlap, what shapes can the overlapping region make?

On a full page in the back of your exercise book draw a perfectly regular pentagon.

Solve the riddle to find the name of the polygon then sum the interior angles.

A "My first is in..." type riddle leading to a polygon interior angle calculation.

A 'My first is in...' riddle that describes a geometrical shape. Can you construct it?

Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.

Can you draw 4 straight lines, without taking your pencil off the paper, which pass through all 9 roses?
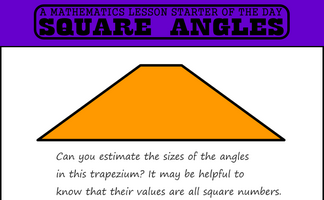
Find a trapezium, a triangle and a quadrilateral where all of the angles are square numbers.

Write down the names of all the mathematical shapes you know.

Separate three rows of three animals using three squares.
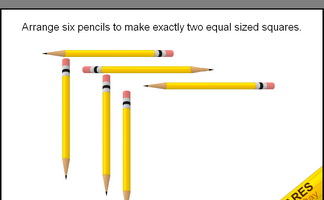
Using six pencils can you make two equal sized squares?
Exercises
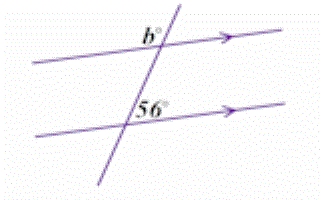
Angle Parallels
Understand and use the relationship between parallel lines and alternate and corresponding angles.
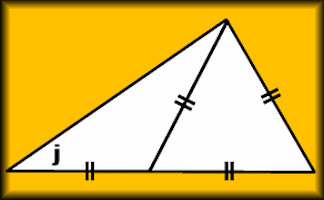
Angles in a Triangle
A self marking exercise involving calculating the unknown angle in a triangle.
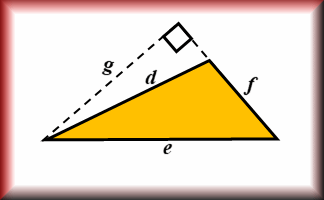
Area and Perimeter
Show that you know the area and perimeter formulas of basic shapes.
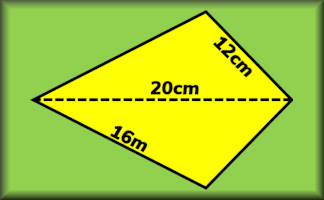
Area and Perimeter of a Kite
A short exercise to practise using the formulae for area and perimeter of a kite.

Area and Perimeter of a Parallelogram
Many different ways to practise your skills finding the areas and perimeters of parallelograms.
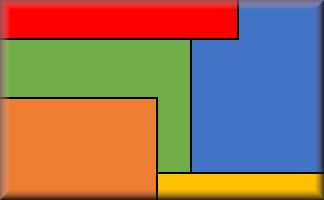
Area and Perimeter of a Rectangle
Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
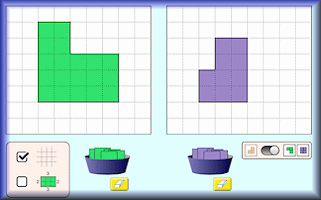
Area Builder
An interactive workspace in which to make shapes using square tiles with given areas and perimeters.
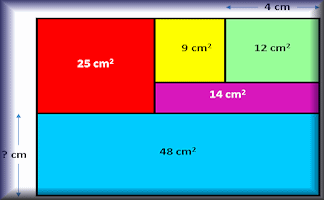
Area Maze
Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.
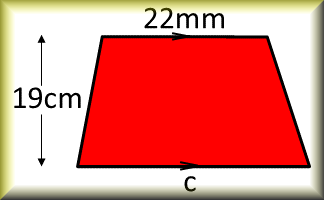
Area of a Trapezium
Check that you can find the area of a trapezium and use the trapezium area formula for problem solving.
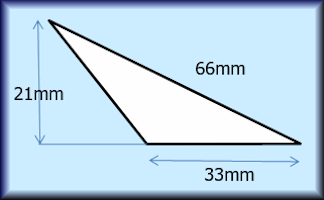
Area of a Triangle
Calculate the areas of the given triangles in this self marking quiz.
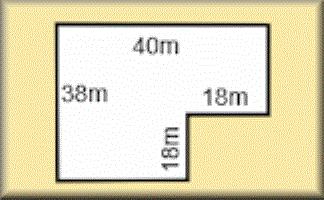
Areas of Composite Shapes
Find the areas of combined (composite) shapes made up of one or more simple polygons and circles.

Circles
Practise using pi to calculate various circle measurements. There are six levels of difficulty.

Congruent Pairs
Match the congruent shapes, those with the same shape and size.
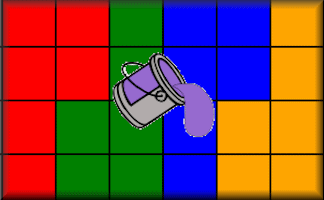
Congruent Parts
Use the colours to dissect the outlines into congruent parts.

Congruent Triangles
Test your understanding of the criteria for congruence of triangles with this self-marking quiz.

Faces, Edges and Vertices
Calculate the number of faces, edges and vertices on 3D Shapes.
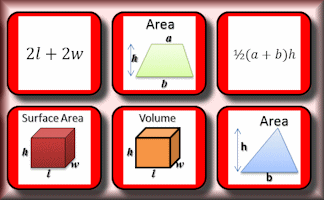
Formulae Pairs
Find the matching pairs of diagrams and formulae for basic geometrical shapes.
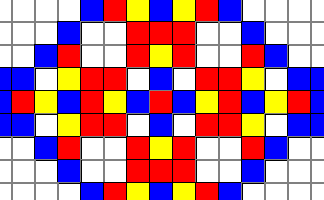
Fractal Mosaic
Follow the precise instructions to create the ever-growing fractal mosaic pattern.
Geometry Toolbox
Create your own dynamic geometrical diagrams using this truly amazing tool from GeoGebra.
How Many Squares? 2
How many different sets of four dots can be joined to form a square?
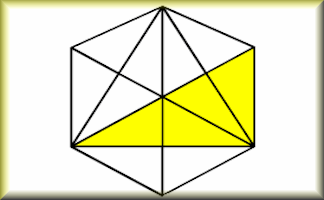
How Many Triangles?
A self marking step by step approach to calculating the number of triangles in a design.

Kite Maths
Can you make a kite shape from a single A4 size sheet of paper using only three folds?
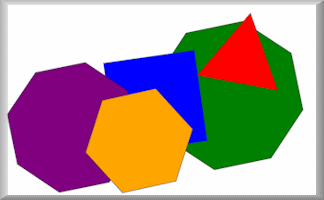
Mathterpieces
Memorise eight pictures made up of geometrical shapes then sort them into order.
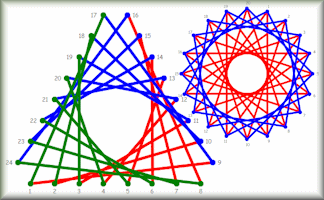
Online Curve Stitching
Create curves with straight lines using this online alternative to needle and thread.
Online Logo
An online version of the Logo programming language with 30 mathematical challenges.

Optical Illusions
Don't let your brain be fooled by these geometric optical illusions in this online quiz.
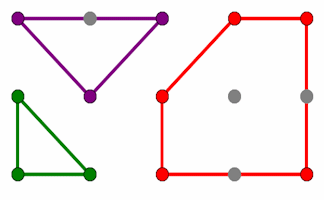
Pin Board
Rows and columns of dots that can be joined using straight lines to create shapes.

Polybragging
The Transum version of the Top Trumps game played online with the properties of polygons.

Polygon Angle Explorer
Barbara Bug walks around a regular hexagon turning through each of the exterior angles as she goes.
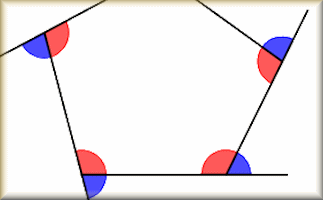
Polygon Angles
A mixture of problems related to calculating the interior and exterior angles of polygons.

Polygon People
Name the polygons and other geometrical shapes that make up the Polygon People.
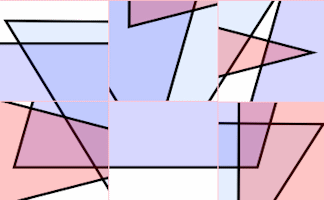
Polygon Pieces
Arrange the nine pieces of the puzzle on the grid to make different polygons.

Polygon Profiles
A visual aid about the properties of regular polygons designed to be projected onto a whiteboard for whole class exposition.

Polygon Properties
Connect the names of the polygons with the descriptions of their properties.
Polygons
Name the polygons and show the number of lines and order of rotational symmetry.
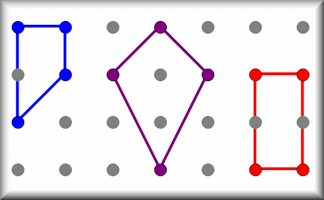
Quad Areas
Calculate the areas of all the possible quadrilaterals that can be constructed by joining together dots on this grid.
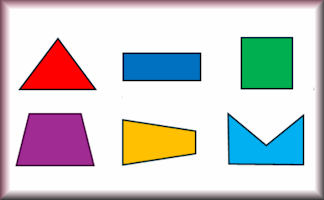
Shape Sorter
Drag each shape into the correct bin according to their types and symmetries.

Shapes In The Stars
Join up the stars to find the hidden regular polygons.
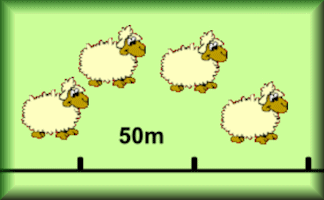
Sheep Herding
Arrange the sheep in the field according to the instructions. An introduction to loci.

Similar Parts
Use the colours to dissect the outlines into similar parts.
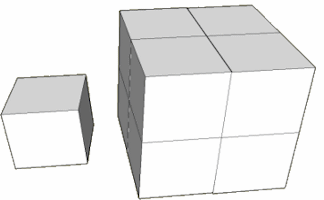
Similar Shapes
Questions about the scale factors of lengths, areas and volumes of similar shapes.

Tangram Challenge
A series of tangram challenges in increasing order of difficulty. This page is designed to be projected onto a screen for a whole class to see.

Tangram Table
Use the pieces of the tangram puzzle to make the basic shapes then complete the table showing which shapes are possible.
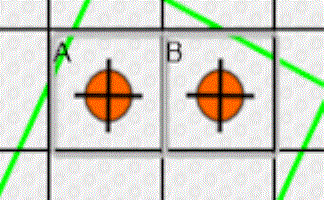
Tantrum
A game, a puzzle and a challenge involving counters being placed at the corners of a square on a grid.
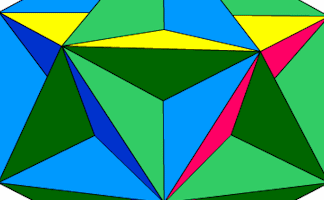
The Great Dodecahedron
Pupils are not allowed to use their hands to point but must describe fully any shapes they can see in this picture.
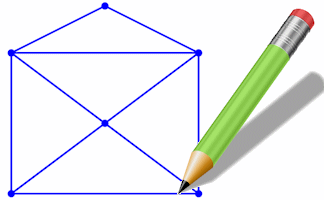
Without Lifting The Pencil
Can you draw these diagrams without lifting your pencil from the paper? This is an interactive version of the traditional puzzle.
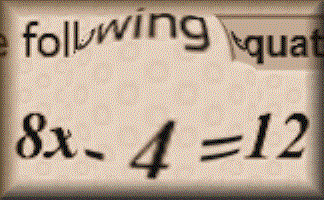
Words and Concepts
Fill in the missing words to show an understanding of the vocabulary of equations, inequalities, angles and shapes.

Xmas Ornaments
A hands on activity requiring students to arrange Christmas ornaments in a square box.

Yes No Questions
A game to determine the mathematical item by asking questions that can only be answered yes or no.
Other activities for this topic | | |
Complete Index of Starters