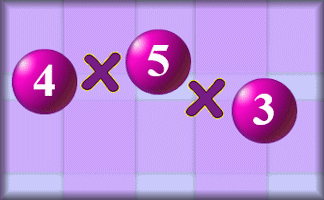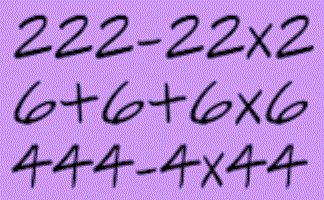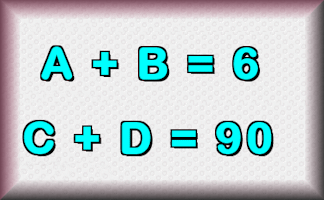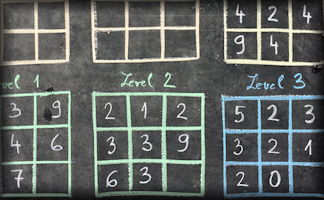Problem Solving Starters:
Add up a sequence of consecutive numbers. Can you find a quick way to do it?

Can you write an expression for 100 which uses all the digits 1 to 9?

How many different shapes with an area of 2 square units can you make by joining dots on this grid with straight lines?

Use only the 1, 5 and 0 keys on a calculator to make given totals.
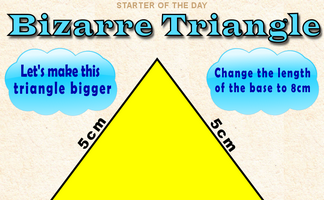
By how much would the area of this triangle increase if its base was enlarged to 8cm?

Work out the contents and the cost of the Christmas boxes from the given clues.

A game in which players take turns to add a single-digit number to what is already in the calculator. The winner is the player who makes the display show 30.

Calculate the total cost of four cars from the information given.

Work out the number of chin ups the characters do on the last day of the week give information about averages.

Work out the total cost of five Christmas presents from the information given.

Can you use the digits on the left of this clock along with any mathematical operations to equal the digits on the right?

A puzzle about the number of coins on a table given information about fractions of them.

Three consecutive numbers multiplied together give a given product. Pupils are asked to figure out what the numbers are.

Which three consecutive numbers multiplied together give the given answer.

How did the clock break if the numbers on each of the pieces added up to the same total?

What numbers should be on each face of the two cubes to make this perpetual calendar?

Determine whether the given nets would fold to produce a dice.
Arrange the digits 1 to 6 to make a three digit number divided by a two digit number giving a one digit answer.
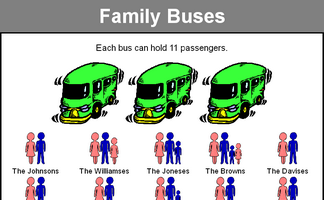
Fit families onto eleven seater buses without splitting up the families.
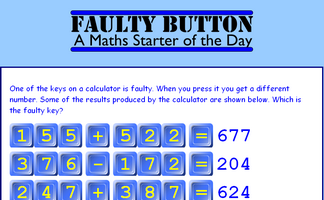
Find out which of the calculator keys is faulty from the given information. A mathematical puzzle requiring good problem solving strategies.

Add up the answers to the four real life questions.

An activity involving a broken calculator which is missing the four button. Can you evaluate the given expressions without using the four?

Which of the numbers from one to twenty can you make with the digits 4, 5, 6 and 7?
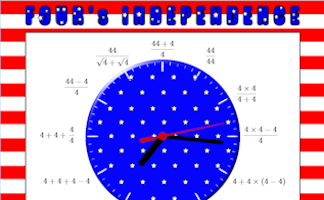
A clock face containing only the number 4. Can you make a clock face containing any other single number?
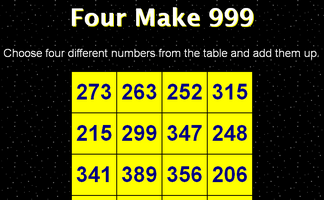
Figure out which numbers will complete the sentences in the frame correctly.
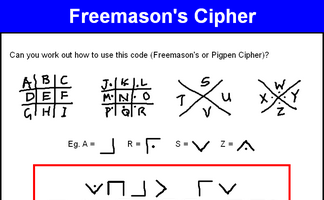
Find symmetric words in this ancient cipher.

The height of this giraffe is three and a half metres plus half of its height. How tall is the giraffe?

If all the students in this room shook hands with each other, how many handshakes would there be altogether?

A little lateral thinking will help you solve this number puzzle.

How many Triangles can you find in the diagram?

How many triangles are hidden in the pattern? What strategy might you use to count them all to ensure you don't miss any out?
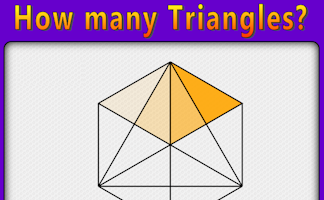
Find a systematic way of counting the number of triangles in the given diagram.

Find a word whose letters would cost exactly ninety nine pence.

Find the weight of one cuboid (by division) of each colour then add your answers together.
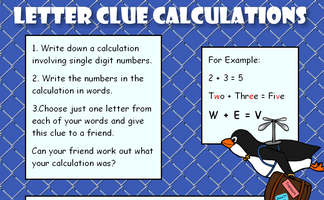
Work out what the calculations might be from the letter clues.

A lamp and a bulb together cost 32 pounds. The lamp costs 30 pounds more than the bulb. How much does the bulb cost?

A classic matchstick puzzle designed to challenge your spacial awareness.

Find which digits are missing from the randomly generated calculations.

A puzzle about a restaurant bill. Exactly where did the missing pound go?

Arrange the digits one to nine to make a correct addition calculation.

Arrange the numbers 1-9 to make three 3 digit numbers that add up to 999.

This activity requires eight students to sit non consecutively on a grid of chairs.

How many ways can you write an expression for 100 which only uses the same digit repeated and any operations?

Two questions involving estimating a quantity.
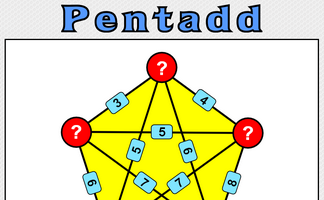
Five numbers are added together in pairs and the sums shown. What might the five numbers be?

Arrange numbers on the plane shaped grid to produce the given totals

If six girls can plant 90 trees in a day. How many trees can ten girls plant in a day? The unitary method.

Arrange the numbers to produce the largest product.

Arrange numbers at the bottom of the pyramid which will give the largest total at the top.

There are some rabbits and chickens in a field. Calculate how many of each given the number of heads and feet.

Use the weights of the trains to work out the weight of a locomotive and a coach. A real situation which produces simultaneous equations.
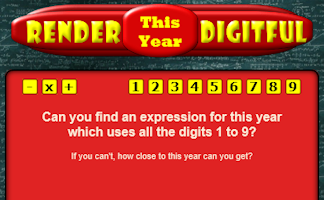
Find a calculation for the current year which uses all of the digits 1 to 9.

Go around the roundabout performing each of the operations. Which starting point gives the largest answer?

Can you draw 4 straight lines, without taking your pencil off the paper, which pass through all 9 roses?

Work out the number of clowns and horses given the number of heads and feet.

A question which can be best answered by using algebra.

Make sums from the three digit numbers given.

Allow two trains to pass by using the limited amount of siding space.

Can you work out what each of the strange symbols represents in these calculations?

The classic game of Nim played with a group of pens and pencils. The game can be extended to the multi-pile version.

A problem which can best be solved as a pair of simultaneous equations.
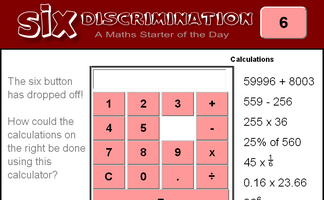
An activity involving a calculator which is missing the six button. Can you evaluate the given expressions without using the six?

Arrange the digits one to nine in the grid so that they obey the row and column headings.

How many different ways can you spell out the word snowman by moving from snowflake to snowflake.

Arrange the numbers on the grid of squares so that the totals along each line of three squares are equal.

Arrange the numbers on the cards so that each of the three digit numbers formed horizontally are square numbers and each of the three digit numbers formed vertically are even.

Arrange the numbered trees so that adjacent sums are square numbers.

Separate three rows of three animals using three squares.
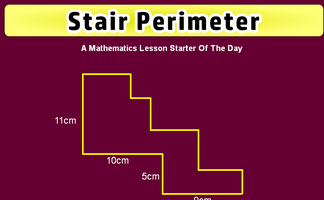
Use the information implied in the diagram to calculate the perimeter of this shape.
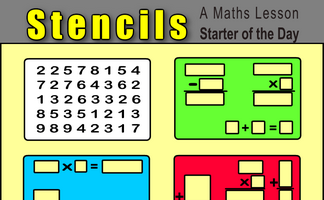
Which of the coloured stencils will fit over the numbered card to produce correct calculations?

Is it possible to work out the perimeter of this shape if not all the side lengths are given?
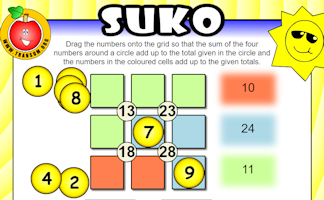
Interactive number-based logic puzzle similar to those featuring in The Times and Telegraph newspapers.

What are the numbers if their sum equals their product?
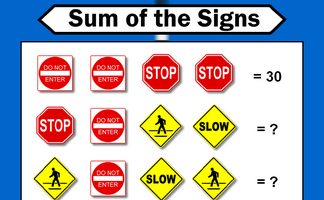
Each traffic sign stands for a number. Some of the sums of rows and columns are shown. What numbers might the signs stand for?
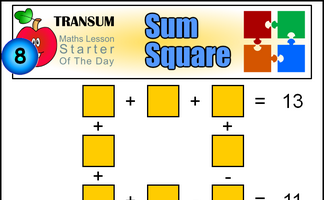
Arrange the numbers one to eight into the calculations to make the totals correct..

Work out who is in which team from the information given.

How can you put the dice into the tins so that there is an odd number of dice in each tin?

In how many different ways might Tran decide to wear his hats in one week?

A tricky problem set on a coordinate grid.

Arrange the numbers 1 to 9 in a 3 by 3 grid so that none of the line totals are the same.

Each letter stands for a different digit. Can you make sense of this word sum?
Advanced Problem Solving Starters
Exercises
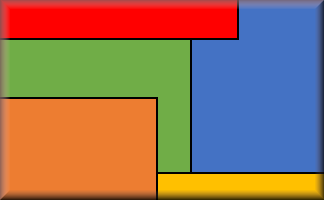
Area and Perimeter of a Rectangle
Questions on the areas and perimeters of rectangles which will test your problem solving abilities.
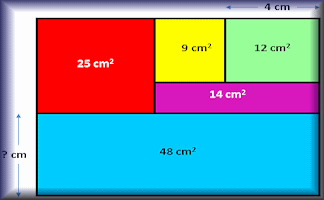
Area Maze
Use your knowledge of rectangle areas to calculate the missing measurement of these composite diagrams.

Area Wall Puzzles
Divide the grid into rectangular pieces so that the area of each piece is the same as the number it contains.
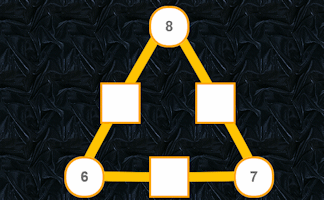
Arithmagons
Find the missing numbers in these triangular, self-checking puzzles and discover the wonders of these fascinating structures.
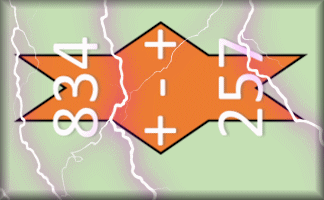
Awe-Sum
Arrange the given digits to make six 3-digit numbers that combine in an awesome way.
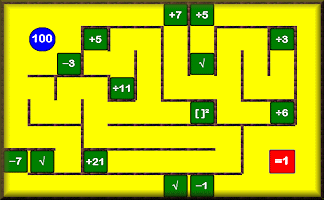
Bidmaze
Find your way through the maze encountering mathematical operations in the correct order to achieve the given total.
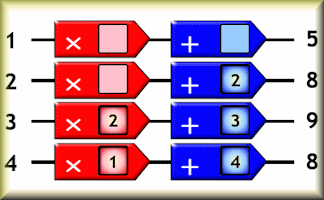
Brainbox
A puzzle requiring the arrangement of numbers on the function machines to link the given input numbers to the correct output.

Broken Calculator
Some of the buttons are missing from this calculator. Can you make the totals from 1 to 20?

Camp Bosrow
Place the camping items into the plots on the camp site according to the clues given.

Car Park Puzzle
Can you get your car out of the very crowded car park by moving other cars forwards or backwards?

Centexpression
Arrange the numbers from 1 to 9 to make an expression with a value of 100.

Chinese Numbers Jigsaw
An online interactive jigsaw puzzle of a grid of Chinese number symbols.
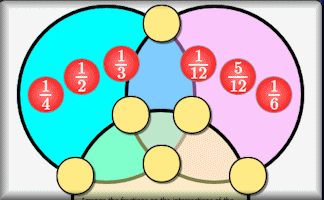
Circumfraction
Quite a challenging number placing puzzle involving fractions.
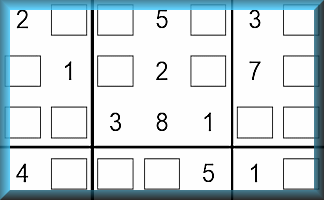
Clue Sudoku
A different way to complete a Sudoku puzzle with clues available at every stage.

Code Cracker
Crack the code by replacing the encrypted letters in the given text. There are lots of hints provided about code breaking techniques.

Consecutive Numbers
Find the consective numbers that are added or multiplied to give the given totals
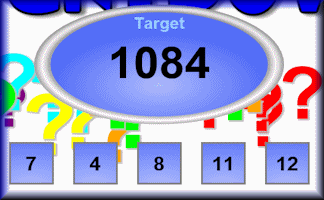
Countdown
How close can you get to the target by making a calculation out of the five numbers given?

Cracked Clock Quiz
A self marking set of ten mathematical questions about a clock which cracked!
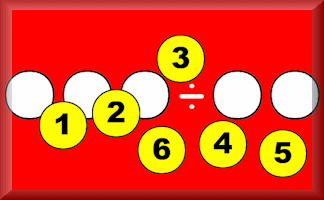
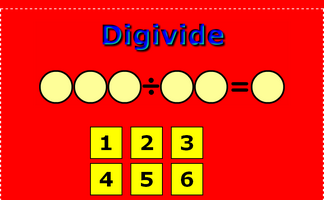
Digivide
Arrange the numbers from 1 to 6 in the spaces to make the division calculation correct.
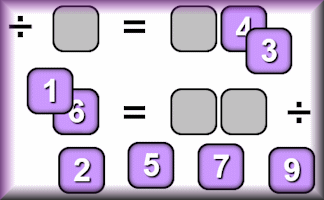
Divisive
Arrange the digits one to nine on the spaces provided to make two division calculations containing multiples of three.

Dominoes Puzzle
Arrange the dominoes in seven squares. The number of dots along each side of the square must be equal to the number in the middle.

Double Treble
Arrange the digits to make three 3 digit numbers such that the second is double the first and the third is three times the first.
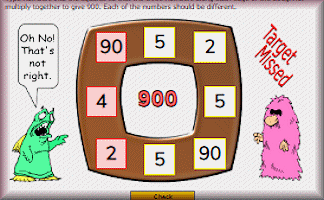
Doughnut Dissection
A puzzle to find four different ways of making 900 by multiplying together three different numbers.

Egg Timers
The classic hourglass puzzle; Time the boiling of an egg using only the two egg timers provided.
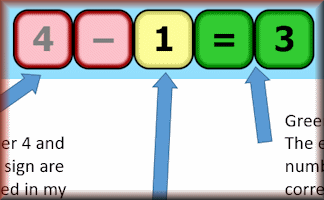
Equatero
Find the expression from a series of guesses and clues.
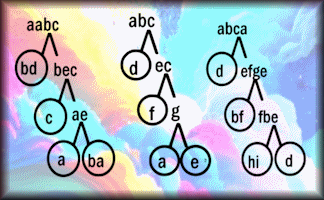
Factor Trees Challenge
Can you determine the unique digits that will complete these factor trees?

Festive Fivesome
Use the number clues to answer the seasonal questions about the five festive figures.

Fleur-De-Lis
Click on six fleur-de-lis to leave an even number in each row and column.
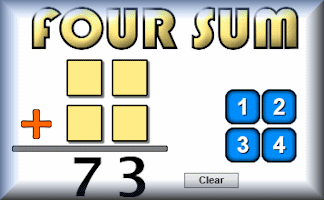
Four Sum
Arrange the given number tiles to make two 2 digit numbers that add up to the given total.

Framed Numbers
Figure out which numbers will complete the sentences in the frame correctly. A drag and drop activity.
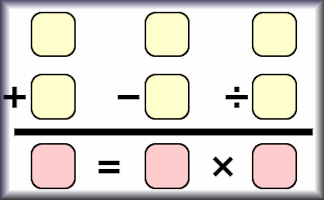
Go Figure
Arrange the digits one to nine to make the four calculations correct.

Goal Products
Arrange the numbered footballs on the goal posts to make three, 3-number products that are all the same.
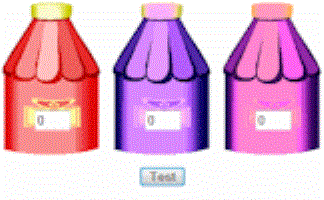
Green Fingers
Choose the amount of liquid from each bottle needed to make the watermelon grow as big as possible.
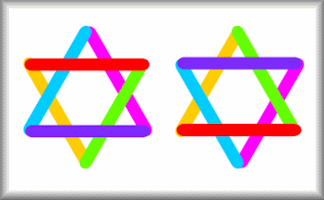
Hexagram Star
Arrange the twelve numbers on the hexagram so that the numbers in each line add up to the same total.

How Many of Each?
Work out how many items were bought from the information given.
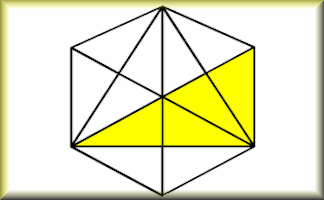
How Many Triangles?
A self marking step by step approach to calculating the number of triangles in a design.

Ice-cream Combinations
How many two-scoop ice creams can you make from the given flavours?

Jugs
Can you make four litres if you only have seven and five litre jugs?
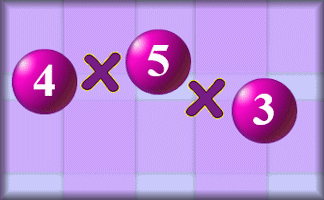
Largest Product
A drag and drop activity challenging you to arrange the digits to produce the largest possible product.

Logic Puzzle
Solve this deduction logic puzzle to find who, where and what.
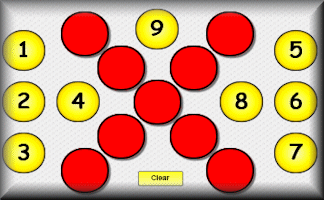
Ludicross
Arrange the given numbers on the cross so that the sum of the numbers in both diagonals is the same.

Magic Square
Each row, column and diagonal should produce the same sum.
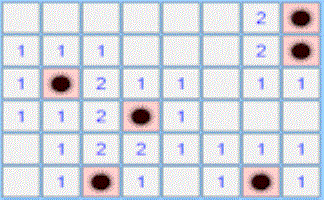
Mine Find
Find where the mines are hidden without stepping on one.
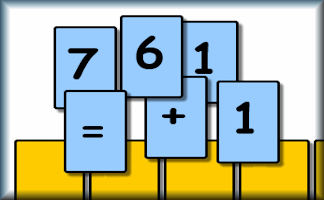
Mixpressions
Arrange the cards to create a valid mathematical statement.

Multi-step Problems
Solve multi-step problems in contexts, deciding which operations and methods to use and why.
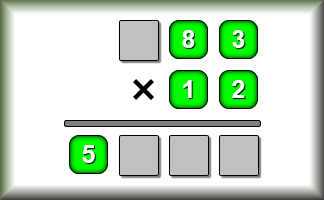
Multitude
Arrange the given digits to make three numbers such that the third is the product of the first and the second.
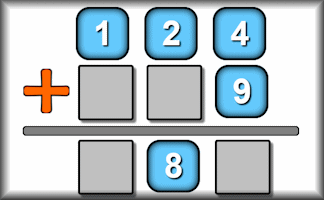
Nine Digits
Arrange the given digits to make three numbers such that two of them add up to the third.
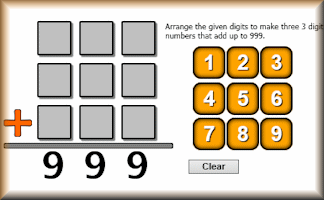
Nine Nine Nine
Use the digits 1 to 9 to make three 3 digit numbers which add up to 999.
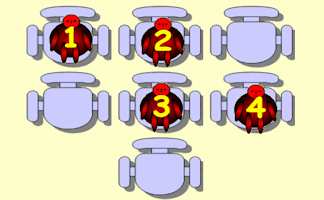
Not Too Close
The students numbered 1 to 8 should sit on the chairs so that no two consecutively numbered students sit next to each other.
Number Jigsaws
Online, interactive jigsaw puzzles of grids of numbers.
Numskull
Interactive, randomly-generated, number-based logic puzzle designed to develop numeracy skills.
Octagram Star
Arrange the sixteen numbers on the octagram so that the numbers in each line add up to the same total.
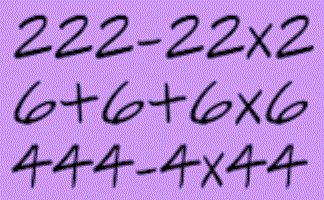
One Digit Only
Find expressions using only one digit which equal the given targets.
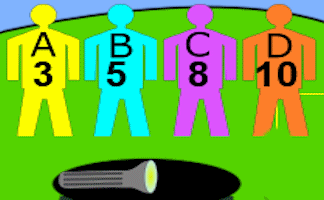
One Torch Tunnel
Solve the problem of getting four people through a tunnel with one torch in the minimum amount of time.

Pancake Day
Toss the pancakes until they are neatly stacked in order of size. Find how to do this using the smallest number of moves.
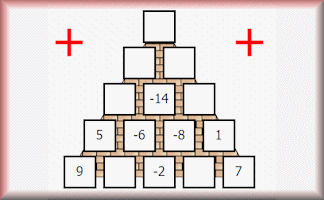
Partial Pyramids
Calculate the missing numbers in these partly completed pyramid puzzles.

Partition Clues
Partition numbers in different ways according to the clues given. The higher levels are quite hard!
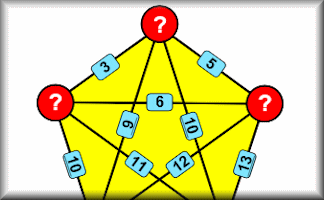
Pentadd Quiz
Find the five numbers which when added or multiplied together in pairs to produce the given sums or products.

Pentominoes
Arrange the twelve pentominoes in the outline of a rectangle.

Perfect Magic Square
Arrange the sixteen numbers on the four by four grid so that groups of four numbers in a pattern add up to the same total.
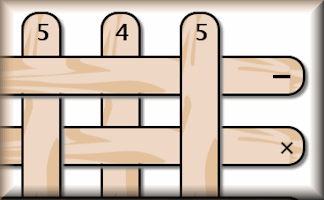
Pick Up Sticks
If you were to pick up the sticks from this pile so that you were always removing the top stick what calculation would you create?

Plane Numbers
Arrange numbers on the plane shaped grid to produce the given totals
Plus
A number arranging puzzle with seven levels of challenge.
Polygon Pieces
Arrange the nine pieces of the puzzle on the grid to make different polygons.
Power Shift
Arrange the given numbers as bases and indices in the three-term sum to make the target total.
Prime Numbers Jigsaw
Interactive jigsaw puzzles of different types of grids containing prime numbers.

Prime Square
Drag the numbers into the red cells so that the sum of the three numbers in each row and each column is a prime number.
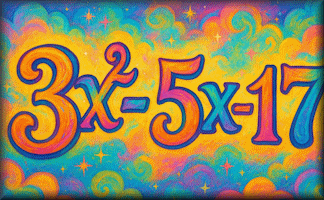
Problems Leading To Quadratics
Situations from 1885 which can be described using algebra and explained by solving quadratic equations
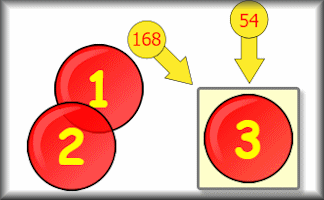
Product Square
Arrange the given numbers in a three by three grid to obtain the diagonal, row and column products.
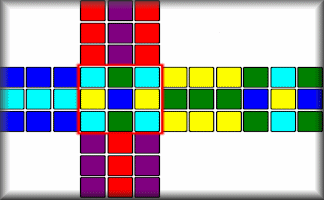
Puzzle Cube Net
A jumbled moving-block puzzle cube is shown as a net. Can you solve it?

Pyramid Puzzle
Numbers in the bricks are found by adding the two bricks immediately below together. Can you achieve the given target?

River Crossing
The traditional River Crossing challenge. Can you do it in the smallest number of moves?
Roman Numerals Jigsaw
An online interactive jigsaw puzzle of a grid of Roman numerals.
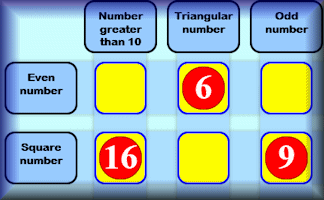
Satisfaction
This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.
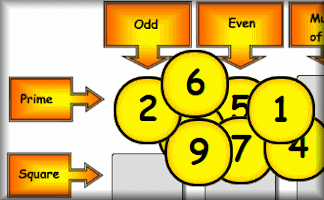
Satisfy
Place the nine numbers in the table so they obey the row and column headings about the properties of the numbers.
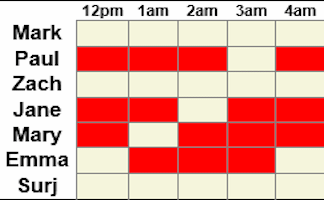
Scheduling Puzzle
Make a schedule for the 24-hour Darts Marathon which will take into account everyone's requests and keep everyone happy.

Scouts in Boats
Arrange a rota for the Scouts to travel in boats so that they are with different people each day.
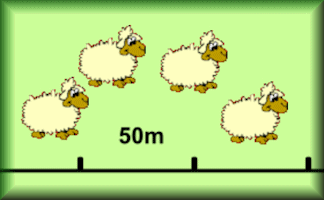
Sheep Herding
Arrange the sheep in the field according to the instructions. An introduction to loci.
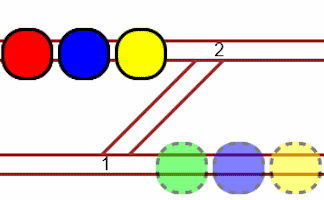
Shunting Puzzles
Move the trams to their indicated parking places in the shunting yard as quickly as possible.

Six Discrimination
The six button has dropped off! How could these calculations be done using this calculator?
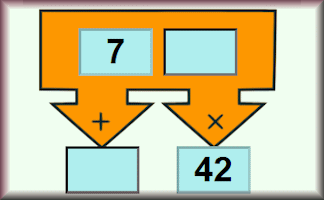
Some Sums and Products
Number puzzles involving adding, multiplying and problem solving

Spinsum
Arrange the numbers on the squares so that the totals along each line of three squares are equal.

Square and Even
Arrange the numbers on the cards so that each of the three digit numbers formed horizontally are square numbers and each of the three digit numbers formed vertically are even.

Squorder
The Transum version of the traditional sliding tile puzzle.
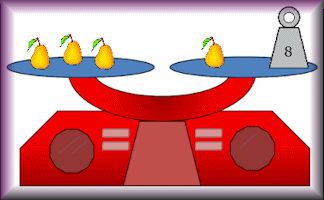
Stable Scales
Ten balance puzzles to prepare you for solving equations.

Suko Sujiko
Interactive number-based logic puzzles similar to those featuring in daily newspapers.
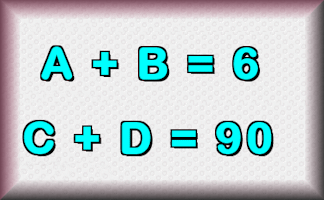
Superfluous
Find a strategy to figure out the values of the letters used in these calculations.
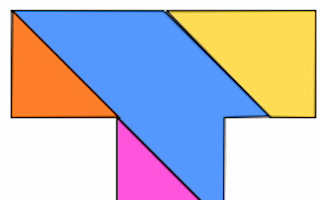
T Puzzle
Use the pieces of the T puzzle to fit into the outlines provided. A drag, rotate and drop interactive challenge.

Tangram Table
Use the pieces of the tangram puzzle to make the basic shapes then complete the table showing which shapes are possible.
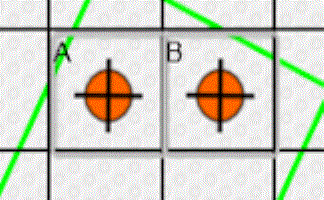
Tantrum
A game, a puzzle and a challenge involving counters being placed at the corners of a square on a grid.

Thai Numbers Jigsaw
An online interactive jigsaw puzzle of a grid of Thai number symbols.
The Miller's Puzzle
This is an interactive version of the puzzle described by Henry Ernest Dudeney in The Canterbury Puzzles
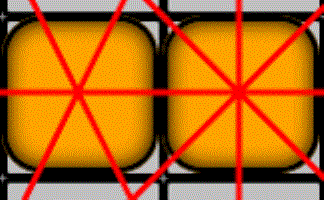
Thrice
A challenge to place all nine counters on the grid in such a way that they form exactly 10 straight lines, with each line containing three counters.
Tools
In how many different ways can the numbers be arranged to give the same totals?

Tower of Hanoi
Move the pieces of the tower from one place to another in the minimum number of moves.
Trafalgar Square
Solve the number puzzles drawn on the pavement of Trafalgar Square in London.

Tran Towers
An adventure game requiring students to solve puzzles as they move through the old mansion.

Tran Tunnels
A mini adventure game containing maths puzzles and problems. Find your way through the maze of tunnels to find Goldberg's magic harpsicord.
Trial And Improvement
Learn efficient ways of using trial and improvement to solve real-life and algebraic problems.
Triangled Hexagram
Arrange the twelve numbers in the triangles on the hexagram so that the numbers in each line of five triangles add up to the same total.
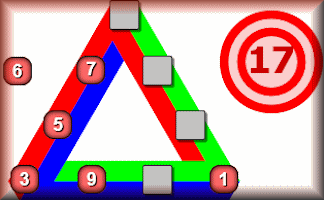
Triside Totals
Arrange the digits 1 to 9 on the triangle so that the sum of the numbers along each side is equal to the given total.

Unbeknownst
Some picture grid puzzles which can be solved by using simultaneous equations.
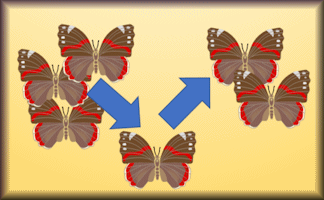
Unitary Method
Ten questions which can be solved using the unitary method.
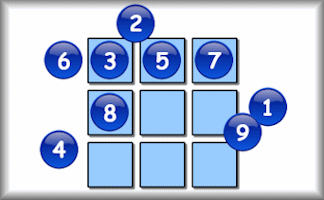
Unmagic Square
Like the magic square but all of the totals should be different.
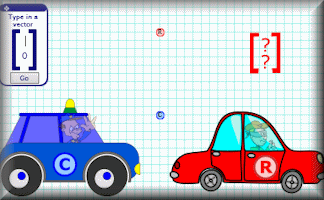
Vector Cops
Help the cops catch the robbers by finding the vectors that will end the chase.

Where's Wallaby?
Find the hidden wallaby using the clues revealed at the chosen coordinates.

Which Operation?
Decide which mathematical operation is required then use it to find the answers.

Window View
Drag the 20 flowers into the gardens so that 9 flowers are visible from each window of the house.

Word Sums Guide
A step by step guide showing how to solve a Word Sum where each letter stands for a different digit.
Other activities for this topic | | |
Complete Index of Starters