
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher [484] |
There are only crayons in a pencil case and the crayons are either orange, purple or brown.
The table shows the probability of taking at random a brown crayon from the pencil case.
| Colour: | orange | purple | brown |
|---|---|---|---|
| Probability: | 0.4 |
The number of orange crayons in the pencil case is the same as the number of purple crayons.
(a) Complete the table.
There are 20 brown crayons in the pencil case.
(b) Work out the total number of crayons in the pencil case.
2. | GCSE Higher [317] |
The following table shows the probabilities of winning certain prizes at a stall in Faulton Towers theme park. A prize is always given for every turn.
| Prize | Pencil | Calculator | Teddy Bear | Ball | Protractor |
|---|---|---|---|---|---|
| Probability | 0.65 | 0.02 | 0.05 | 0.26 | ? |
In the last year Simon has had 200 turns receiving 200 prizes.
Work out an estimate for the total number of times he has won either a pencil or a protractor.
3. | GCSE Higher [442] |
During a demonstration for Year 10 pupils a biased coin in a computer simulation landed on heads 600 times.
The relative frequency of heads was 0.3
Work out the number of times the coin landed on tails during that demonstration.
4. | GCSE Higher [226] |
A bag contains balls that are red, blue, green or yellow.
A counter is chosen at random. The probability it is green is \( \frac{7}{52} \)
Work out the probability it is red.
5. | IB Analysis and Approaches [707] |
On a Tuesday at a theme park, a sample of 50 visitors was randomly selected as they were leaving the park. They were asked how many times that day they had been on a ride called The Serpent. This information is summarised in the following frequency table.
| Number of times on The Serpent | Frequency |
|---|---|
| 0 | 6 |
| 1 | 12 |
| 2 | 17 |
| 3 | 10 |
| 4 | 5 |
It can be assumed that this sample is representative of all visitors to the park for the following day.
(a) For the following day, Wednesday, estimate
(i) the probability that a randomly selected visitor will ride The Serpent;
(ii) the expected number of times a visitor will ride The Serpent.
It is known that 2000 visitors will attend the amusement park on Wednesday. The Serpent can carry a maximum of 18 people each time it runs.
(b) Estimate the minimum number of times The Serpent must run to satisfy demand.

6. | IB Standard [365] |
A game at a fayre consists of a players throwing one dart at the board pictured below.
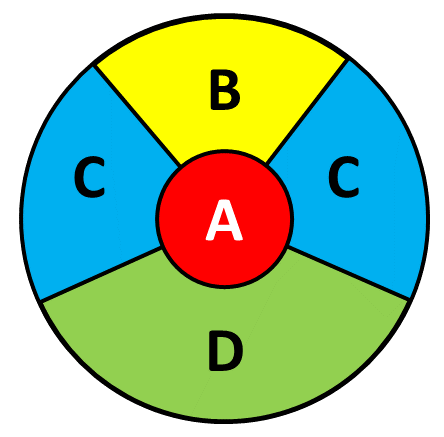
The probability of hitting each region and the points scored for hitting that region is given in this table.
| Region | Probability | Points |
|---|---|---|
| A | \(\frac{1}{25}\) | 50 |
| B | \(\frac{2}{25}\) | \(x\) |
| C | \(\frac{4}{25}\) | 20 |
| D | \(\frac{5}{25}\) | 10 |
(a) Find the probability that the dart does not hit the board.
The player scores points as shown in the table above but they lose 20 points if they miss the board completely.
(b) Given that the game is a fair game, find the value of \(x\), the number of points awarded for hitting the B region of the board.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.