Positions and Direction
Term 3 starting in week 4 :: Estimated time: 1 weeks
- The first quadrant
- Four quadrants
- Translations
- Reflections
This page should remember your ticks from one visit to the next for a period of time. It does this by using Local Storage so the information is saved only on the computer you are working on right now.
Activities for pupils
Here are some related resources in alphabetical order. Some may only be appropriate for high-attaining learners while others will be useful for those in need of support. Click anywhere in the grey area to access the resource.
Transformations Video A demonstration of the four basic transformations: reflection, translation, rotation and enlargement.
Which Transformation? Identify which simple transformations these diagrams represent.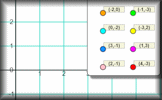
Coordinate Plotter Drag the given points so that they are in the correct positions according to their coordinates.
Coordinates Picture Plot the coordinates and join them with straight lines to produce a picture.
Coordinates Video For those who would like a reminder about coordinates here it is. This video is to help you do the online, self-marking exercises
Coordinates A self marking exercise on identifying coordinates culminating in finding the mid point of two given points.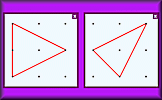
Tridots Find all the triangles that can be drawn by joining dots on a 3 by 3 grid of dots.
Transformations Draw transformations online and have them instantly checked. Includes reflections, translations, rotations and enlargements.
Where's Wallaby? Find the hidden wallaby using the clues revealed at the chosen coordinates.
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Coordinates It is important that pupils become proficient at understanding coordinates at a basic level before using them in their study of graphs. Plotting points and finding the coordinates of points are the pre-requisite skills for studying a number of branches of mathematics. The Cartesian plane consists of a horizontal x-axis and a vertical y-axis that intersect at the origin (0, 0). The mathematician René Descartes developed the concept of the Cartesian plane while lying in bed one morning and observing a fly on the ceiling! Pupils should learn the conventions starting with knowing that the horizontal axis is the x-axis and the vertical axis is the y-axis (remember x is a cross so the x axis is across!). The axes meet at the origin which has coordinates (0,0). Coordinates are written as two numbers separated by a comma and contained inside brackets. For example (3,9) means the point is above 3 on the x-axis and level with 9 on the y-axis. To get to this point from origin you go along 3 and up 9 (remember to go along the hall before going up the stairs or that pole vaulter has to run along before leaping up into the air!). Coordinates can be positive or negative (remember points to the right of the origin have a positive x-coordinate – being positive is right!). The abscissa often refers to the horizontal coordinate of a point and the ordinate refers to the vertical coordinate. In three dimensions, three perpendicular lines are defined as the axes and the coordinates of each point is defined with three numbers.
- Transformations A transformation in mathematics is an operation performed on a shape (or points) which changes the view of that shape (or points). This topic includes four transformations namely reflection, translation, rotations and enlargement. A reflection can best be described as the mirror image of a shape in a given line (which acts as the mirror). After reflection the shape remains the same size but the orientation is the mirror image of the original. The transformation known as a translation can be thought of as a movement or shift in position. The size and orientation of the shape remains the same but the position on the plane changes. A rotation can be described as turning. This transformation is defined by the angle of turning and the centre of rotation (the point which does not move during the turning). Finally enlargement is the term we use when a shape increases in size but maintains the same shape. The shape after enlargement is defines as being similar to the shape before enlargement. His use of the word similar has a precise mathematical meaning. All of the angles in the enlarged shape are the same as the angles in the original shape and the lengths of the sides are in the same proportion. An enlargement is defines by the scale factor of the enlargement and the centre of enlargement. We use the term enlargement even if the shape becomes smaller (a scale factor between minus one and one). A negative scale factor will produce an enlarged mirror image of the original shape.
Lesson Starters
Here are some suggestions for whole-class, projectable resources which can be used at the beginnings of each lesson in this block.
1st Lesson
Graph Picture
Plot the given coordinates then join them up to form a picture.
2nd Lesson
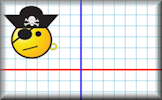
Reflective Cat
On squared paper copy the drawing of the face then reflect it in three different lines.
3rd Lesson
Christmas Ornaments
A Maths Starter activity requiring students to arrange Christmas ornaments in a square box.
Some of the Starters above are to reinforce concepts learnt, others are to introduce new ideas while others are on unrelated topics designed for retrieval practice or and opportunity to develop problem-solving skills.
