Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations.
Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations. Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication.
Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication. Logarithms Video Revise all you need to know in order to complete the Logarithms online exercise.
Logarithms Video Revise all you need to know in order to complete the Logarithms online exercise.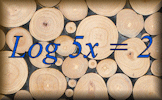 Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.
Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.
Here are some exam-style questions on this statement:
- "If a, b and c are positive integers use the following statements to find the values of a, b and c." ... more
- "It is given that \( \log_{10} x = \frac{1}{4} \), where \( x > 0 \)." ... more
- "Find the value of the following:" ... more
- "Evaluate the following, giving your answers as integers." ... more
- "Find the value of" ... more
- "In an old science fiction book the author described the intensity of reverse polarity, \(P\) measured in treckons, is a function of the nebula thrust, \(N\) measures in whovians. The intensity level is given by the following formula." ... more
- "(a) Solve \(4x^2 - 8x - 5 = 0\)" ... more
- "(a) Show that \( \log_4 (\sin 2x +2) = \log_2 \sqrt{\sin 2x + 2 }\)" ... more
- "An arithmetic sequence has \(u_1 = \log_h(j)\) and \(u_2 = \log_h(jk)\), where \(h > 1\) and \(j, k \gt 0\)." ... more
- "Consider the function \(f (x) = \log_p(24x - 18x^2)\) , for \(0 \lt x \lt 1\), where \(p \gt 0\)." ... more
- "Two functions are defined as follows: \(f(x) = 2\ln x\) and \(g(x) = \ln \frac{x^2}{3}\)." ... more
Here are some Advanced Starters on this statement:
- Index Equation
Solve x squared equals sixteen to the power of x more - Log Perfection
Determine whether the given statements containing logarithms are true or false more - Logarithm Equation
Solve an equation containing logarithms with different bases more - Product of Indices
Find the product of the unknown indices that feature in two equations more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
The laws of exponents with rational exponents allow us to simplify and manipulate expressions involving powers. These laws are fundamental in algebra and are used to solve a variety of mathematical problems. Similarly, logarithms provide a way to undo exponential functions and have their own set of laws that make calculations more straightforward. The change of base formula for logarithms is particularly useful when working with logarithms of different bases. Solving exponential equations often involves using logarithms to rewrite and solve the equation.
Laws of Exponents with Rational Exponents:
1. Product of Powers: \( a^m \times a^n = a^{m+n} \)
2. Quotient of Powers: \( \frac{a^m}{a^n} = a^{m-n} \)
3. Power of a Power: \( (a^m)^n = a^{mn} \)
4. Power of a Product: \( (ab)^n = a^n b^n \)
5. Negative Exponent: \( a^{-n} = \frac{1}{a^n} \)
6. Rational Exponent: \( a^{\frac{m}{n}} = \sqrt[n]{a^m} \)
Example: Simplify \( 2^{\frac{3}{2}} \times 2^{\frac{1}{2}} \)
Using the Product of Powers rule:
\( 2^{\frac{3}{2}} \times 2^{\frac{1}{2}} = 2^{\frac{3}{2} + \frac{1}{2}} = 2^2 = 4 \)
Laws of Logarithms:
1. Product Rule: \( \log_b(mn) = \log_b(m) + \log_b(n) \)
2. Quotient Rule: \( \log_b\left(\frac{m}{n}\right) = \log_b(m) - \log_b(n) \)
3. Power Rule: \( \log_b(m^n) = n \cdot \log_b(m) \)
Change of Base Formula:
For any positive numbers \( a \), \( b \), and \( c \) where \( a \neq 1 \) and \( b \neq 1 \):
\[ \log_b(c) = \frac{\log_a(c)}{\log_a(b)} \]
Example: Express \( \log_2(8) \) in terms of natural logarithm (base \( e \)):
Using the Change of Base Formula:
\[ \log_2(8) = \frac{\ln(8)}{\ln(2)} \]
Solving Exponential Equations:
To solve \( b^x = c \) for \( x \), take the logarithm of both sides:
\[ \log{(b^x)} = \log{(c)} \]
\[ x\log{(b)} = \log{(c)} \]
\[ x = \frac{\log(c)}{\log(b)} \]
Example: Solve \( 2^x = 8 \) for \( x \):
Taking the logarithm of both sides:
\[ x = \frac{\log(8)}{\log(2)} = \frac{\log(2^3)}{\log(2)} = \frac{3\log(2)}{\log(2)} = 3 \]
This video on Exponent Laws and Solving Equations is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
This video on Exponential and Logarithmic Functions is from Revision Village and is aimed at students taking the IB Maths AA Standard level course.
This video on Log Laws and Solving Equations is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
Transum,
Saturday, August 17, 2019
"Just when you thought you'd mastered all of the laws of logarithms this Advanced Lesson Starter called Log Perfection will shake your confidence. Not for the feint-hearted!"
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

