Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 What is a Function? This A-Level Maths video introduces functions, explaining their core concept: one input, one output.
What is a Function? This A-Level Maths video introduces functions, explaining their core concept: one input, one output. Functions An online exercise on function notation, inverse functions and composite functions.
Functions An online exercise on function notation, inverse functions and composite functions.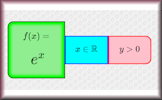 Domain, Range and Asymptotes Match the functions with their features. A drag and drop activity.
Domain, Range and Asymptotes Match the functions with their features. A drag and drop activity.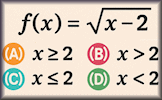 Domain and Range Find the domain and range of various functions expressed in different ways
Domain and Range Find the domain and range of various functions expressed in different ways
Here are some exam-style questions on this statement:
- "Given the function:" ... more
- "(a) A function is represented by the following function machine." ... more
- "Here is a function machine that produces two outputs, A and B." ... more
- "The circumference of a given circle \(C\) can be represented by the function \(C(A) =2\sqrt{A \pi}, A \ge 0 \) where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 16\)." ... more
- "The diagram shows the graph of \(y=f(x)\), for \(-3\le x \le 4\)." ... more
- "The circumference of a given circle \(C\) can be represented by the function \(C(A) = 2 \sqrt{A \pi}\) , \(A \ge 0 \) , where \(A\) is the area of the circle. The graph of the function \(C\) is shown for \(0 \le A \le 10\)." ... more
- "Consider the function \(f(x) = k^x \) where \(x, k \in \mathbb{R}\) and \( x \gt 0, k > 1\)." ... more
- "A function \( g \) is defined by \( g(x) = \frac{3x - 10}{x^2 - 9} \), where \( x \in \mathbb{R} \), \( x \neq \pm3 \)." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
In mathematics, a function is a relationship between a set of inputs and a set of permissible outputs. The domain of a function is the set of all possible inputs, while the range is the set of all possible outputs. Function notation, such as \( f(x) \), is used to denote a function \( f \) applied to an input \( x \). The graph of a function is a visual representation of this relationship, plotting inputs versus outputs.
An inverse function reverses the effect of a given function. If a function \( f \) takes an input \( x \) and produces an output \( y \), then its inverse \( f^{-1} \) takes \( y \) as input and returns \( x \) as output. Graphically, the inverse function is a reflection in the line \( y = x \).
Key Formulae:
$$ \begin{align*} \text{Function: } & f(x) \\ \text{Domain: } & \{x \,|\, \text{conditions on } x\} \\ \text{Range: } & \{f(x) \,|\, x \in \text{Domain of } f\} \\ \text{Inverse Function: } & f^{-1}(y) \text{ such that } f(f^{-1}(y)) = y \end{align*} $$Example:
$$ \begin{align*} \text{Let } f(x) &= x^2, \text{ for } x \geq 0 \\ \text{Domain: } & [0, \infty) \\ \text{Range: } & [0, \infty) \\ f^{-1}(y) &= \sqrt{y}, \text{ for } y \geq 0 \\ \text{Thus, } f^{-1}(f(x)) &= f^{-1}(x^2) = \sqrt{x^2} = x \end{align*} $$If you use the TI-Nspire calculator you can find instructions for defining a function on the GDC Essentials page. Ver useful if you need to evaluate the function for different x-values and plot a graph of the function.
This video on Functions: Overview and Types is from Revision Village and is aimed at students taking the IB Maths AI Standard level course.
This video on Domain, Range, Composite, Inverse is from Revision Village and is aimed at students taking the IB AA Maths Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

