International Baccalaureate Mathematics

Syllabus Content

Exponential functions and their graphs: f(x)=a^x, a>0, f(x)=e^x. Logarithmic functions and their graphs: f(x)=log_ax, x>0, f(x)=lnx, x>0

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

What is e? Dr James Grime discusses e - the famed Euler's Number.

Indices A self marking exercise on indices (powers or exponents) including evaluating expressions and solving equations.

Indices Video Indices, exponents and powers can all be used as a short way to describe repeated multiplication.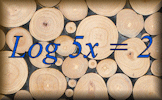

Logarithms Self-marking exercises on evaluating logarithms and using them to solve equations.

Here are some exam-style questions on this statement:

"Sketch the graph of $y=0.5^x +1$ for $0 \le x \le 5$ labeling the y intercept." ... more

"While studying a new disease, scientists found that the number of toxic cells in the bloodstream increased over time, according to the model $D(t)=12×(1.16)^t , t \ge 0$ where $D$ is the number of the toxic cells in the bloodstream per litre and $t$ is the time in hours." ... more

"Percy Cod and Fran Finklestein are both researchers working at different universities. They are each studying a different colony of bacteria which coincidentally start increasing in size at the same time." ... more

"The diagrams above show a growing fractal of triangles. The sides of the largest equilateral triangle in each diagram are of length 1 metre." ... more

"The quantity of heat required to heat an amount of water is given by the formula:" ... more

"Consider the following function for $-2 \le x \le 2$." ... more

"Find the value of the following:" ... more

"Evaluate the following, giving your answers as integers." ... more

"Find the value of" ... more

"(a) Solve $4x^2 - 8x - 5 = 0$" ... more

"In medical imaging, the radioactive isotope Technetium-99m is used due to its short half-life of 6 hours. After being introduced into the body, the isotope decays, and the amount of Technetium-99m present can be tracked over time to study the function of specific organs." ... more

"A cup of hot tea is placed on a table to cool. The temperature of the room is 24^oC." ... more

"In a remote lake it was noticed by conservationists that a disease was rapidly spreading amongst two species of fish, R and S, which is reducing their numbers. The conservationists calculated that the numbers of each type of fish can be modelled by the functions:" ... more

"Consider the function $f (x) = \log_p(24x - 18x^2)$ , for $0 \lt x \lt 1$, where $p \gt 0$." ... more

"Fifty milligrams of a certain type of medicine has been shown to enter the bloodstream of an adult according to the following equations:" ... more

See all these questions

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Logarithms Older teachers will remember their school days, before calculators were widely available, using logarithms to perform difficult multiplication and division calculations. Nowadays logarithms, or logs as they are more commonly known, are studied as part of an A Level and International Baccalaureate course and are seen as being useful for solving certain exponential equations. Basically a logarithm is the inverse function to exponentiation.

Furthermore

Official Guidance, clarification and syllabus links:

Link to: financial applications of geometric sequences and series (SL 1.4).

Relationships between these functions: $a^x=e^{x\ln{a}}; \quad \log_aa^x=x, \text{ where } a \gt 0, x \gt 0, a\neq 1 $

Exponential and logarithmic functions as inverses of each other.

Formula Booklet:

Exponential and logarithmic functions

$a^x=e^{x\ln{a}}; \quad \log_aa^x=x=a^{\log_ax}, \\ \text{ where } a \gt 0, x \gt 0, a\neq 1 $

Exponential functions, represented as $ f(x) = a \cdot b^x $, where $ a $ and $ b $ are constants, exhibit a rapid increase or decrease as the value of $ x $ changes. The base $ b $ is a positive real number, and when $ b > 1 $, the function shows exponential growth, whereas if $ 0 < b < 1 $, it demonstrates exponential decay. The graph of an exponential function is a curve that either increases or decreases rapidly, but never crosses the x-axis, as it asymptotically approaches the axis. The general form of an exponential function is $$ f(x) = a \cdot b^x, $$ where $ a $ is the initial value, and $ b $ is the base of the exponential.

Logarithmic functions are the inverses of exponential functions. The logarithmic function $ g(x) = \log_b(x) $ is defined such that if $ y = \log_b(x) $, then the equivalent exponential expression is $ x = b^y $. The base $ b $ of the logarithm is the same as the base of the corresponding exponential function. Graphs of logarithmic functions are the reflection of their exponential counterparts across the line $ y = x $. The general form of a logarithmic function is $$ g(x) = \log_b(x), $$ where $ b $ is the base of the logarithm. Logarithmic functions are useful in solving equations where the variable is an exponent in an exponential function.

This video on Exponential and Logarithmic Functions is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.