Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Common Trig Ratios Video You may not realise that it is possible to find sin60° or tan45° without a calculator. This video is to help you do the online, self-marking exercise.
Common Trig Ratios Video You may not realise that it is possible to find sin60° or tan45° without a calculator. This video is to help you do the online, self-marking exercise.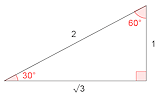 Common Trig Ratios Degrees A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles.
Common Trig Ratios Degrees A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles.
Here are some exam-style questions on this statement:
- "Find the exact value of tan45° × sin30° × cos30°" ... more
- "(a) Write down the exact value of \(\tan 60^o\)." ... more
- "The area of triangle ABC (not drawn to scale) is " ... more
- "The cosine of acute angle \( \alpha \) is \( \frac{1}{ \sqrt 5} \)" ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
In the context of the unit circle, \( \cos\theta \) and \( \sin\theta \) represent the coordinates of a point on the circle's circumference. Specifically, \( \cos\theta \) corresponds to the x-coordinate and \( \sin\theta \) to the y-coordinate for any angle \( \theta \) measured from the positive x-axis. The tangent of an angle, \( \tan\theta \), is defined as the ratio of \( \sin\theta \) to \( \cos\theta \).
Key formulae:
\[
\begin{align*}
\sin\theta &= \frac{\text{opposite}}{\text{hypotenuse}} \\\\
\cos\theta &= \frac{\text{adjacent}}{\text{hypotenuse}} \\\\
\tan\theta &= \frac{\sin\theta}{\cos\theta} = \frac{\text{opposite}}{\text{adjacent}} \\\\
\end{align*}
\]
The trigonometric ratios for specific angles are as follows:
| Radians | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) |
|---|---|---|---|---|---|
| Degrees | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) |
| \(\sin\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
| \(\cos\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | \(0\) |
| \(\tan\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) | Undefined |
When dealing with the sine rule, especially in its extended form for the ambiguous case, we use the formula:
\[
\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}
\]
where \( A \), \( B \), and \( C \) are the angles of a triangle, and \( a \), \( b \), and \( c \) are the lengths of the sides opposite those angles, respectively.
This ParkerMaths video gives a clear concise explanation of the Unit Circle.
This video on Unit Circle and Trig Ratios is from Revision Village and is aimed at students taking the IB Maths AA SL and HL Standard level course
This video on Solving Trig Functions and Equations is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course.
Transum,
Saturday, August 17, 2019
"Here's an Advanced Lesson Starter that is just right to present to a class when they are learning exact values of common angles. It is a challenge to find the Tangent of 22.5o without using a calculator but a helpful diagram is included."
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

