International Baccalaureate Mathematics

Syllabus Content

The circular functions sinx, cosx, and tanx; amplitude, their periodic nature, and their graphs. Composite functions of the form f(x)=asin(b(x+c))+d. Transformations. Real-life contexts

Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.

Inverse Trig Calculator This calculator is designed to find all of the angles for a given trigonometric ratio and show them on a graph.

Here are some exam-style questions on this statement:

"Consider the graph of $f(x)=a\sin(b(x+c))+12$, for $0\le x\le 24$." ... more

"The diagram shows part of the graph of $y=a\sin{(bx)}+c$ with a minimum at $(-2.5,-2)$ and a maximum at $(2.5,4)$." ... more

"The Big Wheel at Fantasy Fun Fayre rotates clockwise at a constant speed completing 15 rotations every hour. The wheel has a diameter of 90 metres and the bottom of the wheel is 6 metres above the ground." ... more

"The population of sheep on a ranch is modelled by the function $P(t)= 65 \sin(0.4t-32)+450$, where t is in months, and $t=1$ corresponds to 1st January 2015." ... more

"The Fun Wheel at the Meller Theme Park rotates at a constant speed." ... more

"(a) Sketch the graph of $f(x) = 4\sin x - 5\cos x $, for $–2\pi \le x \le 2\pi $." ... more

"Let $f(x)=\sin ( \frac {\pi}{4}x) + \cos ( \frac {\pi}{4}x) $, for $-4\le x \le 4$" ... more

"Consider a function $f$, such that $f(x)=7.2\sin(\frac{\pi}{6}x + 2) + b$ where $ 0\le x \le 12$" ... more

"A carriage attached to a tall vertical pole in an amusement park ride whisks customers up and down. The height, $H$ metres, of the base of the carriage above the ground can be modelled by the function $H(t) = a\cos(0.4t) + b$, for $a, b \in \mathbb{R}$ and $t$ is the time in seconds after the ride starts." ... more

"The height above the ground, H metres, of a passenger on a Ferris wheel t minutes after the wheel starts turning, is modelled by the following equation:" ... more

"The height of water in metres above Chart Datum* in the Port of Bristol on a day in January is modelled by the function:" ... more

See all these questions

Here are some Advanced Starters on this statement:

Angle Thinking
Find the range of possible angles, x, for which tan x > cos x > sin x more

Tansum
Find the sum of the tangents of angles on a straight line. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Trigonometry Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles. Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules. The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop. Here's a Trigonometry Wordsearch just for fun.

Furthermore

Official Guidance, clarification and syllabus links:

Trigonometric functions may have domains given in degrees or radians.

Examples: $ f(x) = \tan\left(x - \frac{\pi}{4}\right) $,

$ f(x) = 2\cos(3(x - 4)) + 1 $.

Example: $ y = \sin x $ used to obtain $ y = 3\sin 2x $ by a stretch of scale factor 3 in the y direction and a stretch of scale factor $ \frac{1}{2} $ in the x direction.

Link to: transformations of graphs (SL2.11).

Examples: height of tide, motion of a Ferris wheel.

Students should be aware that not all regression technology produces trigonometric functions in the form $ f(x) = a\sin(b(x + c)) + d $.

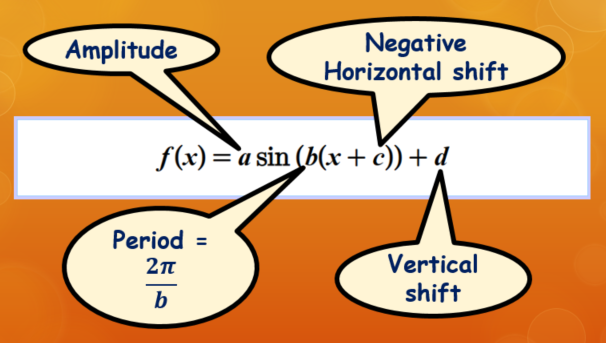
The circular functions sin x, cos x, and tan x represent the fundamental relationships found in a right-angled triangle, extended to all real numbers using the unit circle. They are periodic functions, which means they repeat their values in regular intervals. The amplitude of these functions indicates the maximum value they reach, and this periodic nature allows us to model many real-life phenomena such as sound waves or seasonal patterns. When we graph these functions, they create a wave-like pattern, each with distinctive shapes corresponding to their ratios in the unit circle. Composite functions of the form $ f(x) = a \sin(b(x + c)) + d $ allow for adjustments in amplitude, frequency, phase shift, and vertical shift, enabling a more precise modelling of real-world situations.

Composite trigonometric functions can be transformed to fit specific criteria, useful in both theoretical and practical applications. The 'a' value modifies the amplitude, 'b' affects the period of the function, 'c' adjusts the horizontal shift, and 'd' translates the function vertically. These transformations are essential in applications ranging from physics to engineering, where waves and oscillations describe many different phenomena.

Example: To model the daily hours of daylight over a year at a particular latitude, one might use the function:

$$ f(x) = A \sin\left(\frac{2\pi}{365}(x - \phi)\right) + D $$

where:

$ A $ is the amplitude, representing the maximum deviation from the average daylight hours,
$ B = \frac{2\pi}{365} $ represents the period of the function, reflecting the number of days in a year,
$ \phi $ is the phase shift, corresponding to the day with the least or most daylight,
$ D $ is the average daylight hours over the year.

This video on Trig Graphs and Circular Functions is from Revision Village and is aimed at students taking the IB Maths AA SL/HL course.

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

International Baccalaureate Mathematics

Geometry and Trigonometry

Furthermore