International Baccalaureate Mathematics

Syllabus Content

Definition of the reciprocal trigonometric ratios secθ, cosecθ and cotθ.
Pythagorean identities:
1+tan²θ=sec²θ
1+cot²θ=cosec²θ
The inverse functions f(x)=arcsinx,
f(x)=arccosx,f(x)=arctanx; their domains and ranges; their graphs.

Formula Booklet:

Reciprocal trigonometric identities

$\sec \theta = \frac{1}{\cos \theta}$

$\cosec \theta = \frac{1}{\sin \theta}$

Pythagorean identities

$1 + \tan^2 \theta = \sec^2 \theta$

$1 + \cot^2 \theta = \cosec^2 \theta$

Here is an Advanced Starter on this statement:

Cos 10 Equals p
Find the trigonometric values in terms of the given value, p. more

Click on a topic below for suggested lesson Starters, resources and activities from Transum.

Trigonometry Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles. Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules. The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop. Here's a Trigonometry Wordsearch just for fun.

Furthermore

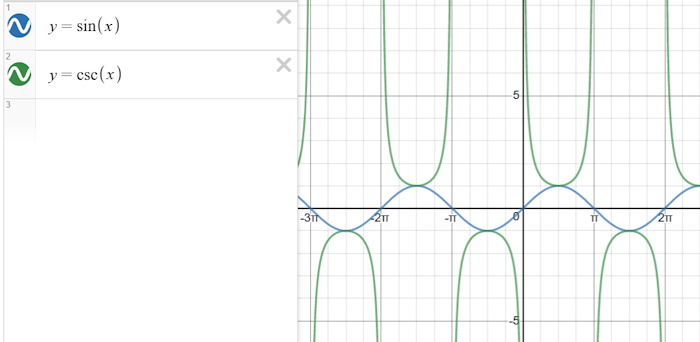
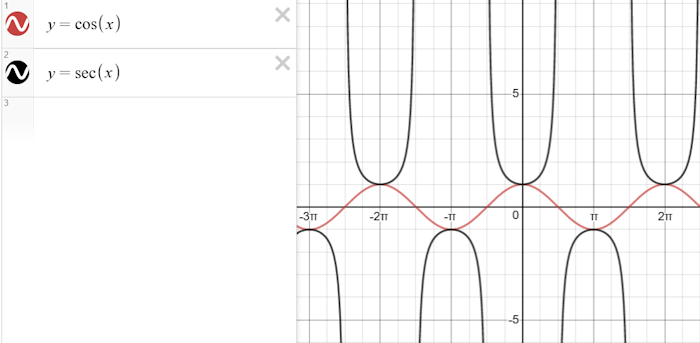
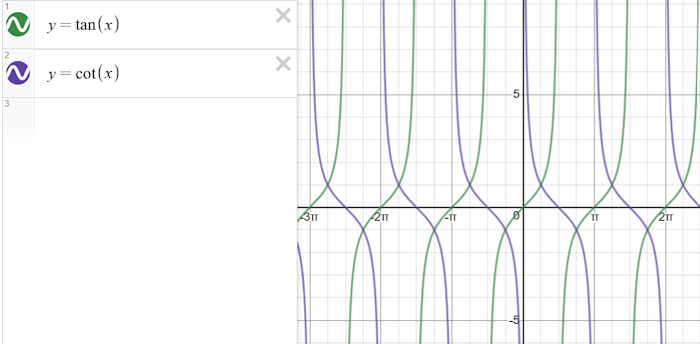
Reciprocal trigonometric ratios are ratios that involve the reciprocal (or multiplicative inverse) of the trigonometric functions. The reciprocal ratios are the cosecant (cosec or csc), secant (sec), and cotangent (cot).

The formulas for the reciprocal ratios are as follows:

$\csc\theta = \frac{1}{\sin\theta} \\ \sec\theta = \frac{1}{\cos\theta} \\ \cot\theta = \frac{1}{\tan\theta} = \frac{\cos\theta}{\sin\theta}$

Here is an example:

Given that $\sin\theta = \frac{3}{5}$ , find the values of $\csc\theta$ , $\sec\theta$ , and $\cot\theta$ .

$\csc\theta = \frac{1}{\sin\theta} = \frac{1}{\frac{3}{5}} = \frac{5}{3}$

$\sec\theta = \frac{1}{\cos\theta} = \frac{1}{\sqrt{1 - \sin^2\theta}} = \frac{1}{\sqrt{1 - \left(\frac{3}{5}\right)^2}} = \frac{5}{4}$

$\cot\theta = \frac{\cos\theta}{\sin\theta} = \frac{\sqrt{1 - \sin^2\theta}}{\sin\theta}$

$= \frac{\sqrt{1 - \left(\frac{3}{5}\right)^2}}{\frac{3}{5}} = \frac{4}{3}$

Therefore, $\csc\theta = \frac{5}{3}$ , $\sec\theta = \frac{5}{4}$ , and $\cot\theta = \frac{4}{3}$ .

Screenshot below taken from Desmos Graphing Calculator (www.desmos.com) Cosec Graph Cot Graph

How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

International Baccalaureate Mathematics

Geometry and Trigonometry

Furthermore