Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of April 2025. The first day of April is April Fools' Day as you probably know. Let me know if your pupils were fooled by the Maths lesson Starter for 1st April called One out of Ten which is not what it seems.
Let's crack on now, as usual, with the puzzle of the month:
I paid £3.60 for the mini Easter eggs I bought from the corner shop. The shop owner added two extra eggs because the best before date was rapidly approaching. That brought the total cost down by 30p per dozen compared to the original price.
How many eggs did I buy?

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at: gro.musnarT@rettelsweN
The answer and the credit for the inspiration for this puzzle will be in next month's Newsletter. While you think about it here are some of the key resources added to the Transum website during the last month.
Statistics Supplied is another one of these exercises that turns around the normal question format. There are three levels requiring pupils to come up with three, four or five numbered sets that obey the information given about mean, median, mode and range. The exercises provide a great opportunity to deepen understanding and develop problem-solving strategies.
Prime Prevention has a two-player mode but what I have found a really interesting activity is the one-player challenge. Arrange the available digits in the cells so that no line of three cells form a prime number.
I tried the challenge myself using my knowledge of the divisibility tests and found myself engrossed in the task. I highly recommend the challenge to you teachers before unleashing it on your pupils.
Division Master is a new activity to promote fast recall of times tables facts. If, however, you need a similar, quick response, division activity that focuses on just one times table at a time try QuotientMaster. Both of these activities can be used alongside the really popular activity called Tablesmaster.
Doon Ow! is the strangest title for a new Starter, but it is pronounced "Do Now" (do you see what I did there?). The projectable page contains a timer and five questions that can be changed by the teacher. Those of you who use Refreshing Revision will notice that it uses the same question bank but the presentation is different. The latter Starter is still the most customisable activity on the whole of the Transum site.
Special dates in April:
1st April - April Fools' Day :: more...
18 April - World Heritage Day :: more...
20 April - Easter Sunday :: more...
In many UK secondary schools, the norm is for students to write most of their classwork in pen, including maths. This practice is partly to ensure neatness and discourage excessive erasing, and indeed, in GCSE exams, students are expected to use pens. Nevertheless, pencils are still used for diagrams and any work where erasing is beneficial.
In contrast, students in the US more commonly use pencils for their maths work, largely because erasing is considered a natural step in problem-solving. Standardised tests in the US often require pencil use, reinforcing this habit. Despite these general trends, practices can vary significantly, even within the same school. I’d love to hear about your approach—do you encourage your students to use pens or pencils, and why?

I'm currently based in Bangkok, Thailand. You've probably heard about the devastating earthquake in neighbouring Myanmar on Friday, which shook the Thai capital and woke me from my early afternoon nap. Luckily, I only suffered cracked bathroom tiles, but my heartfelt condolences go out to the hundreds who were not so fortunate.
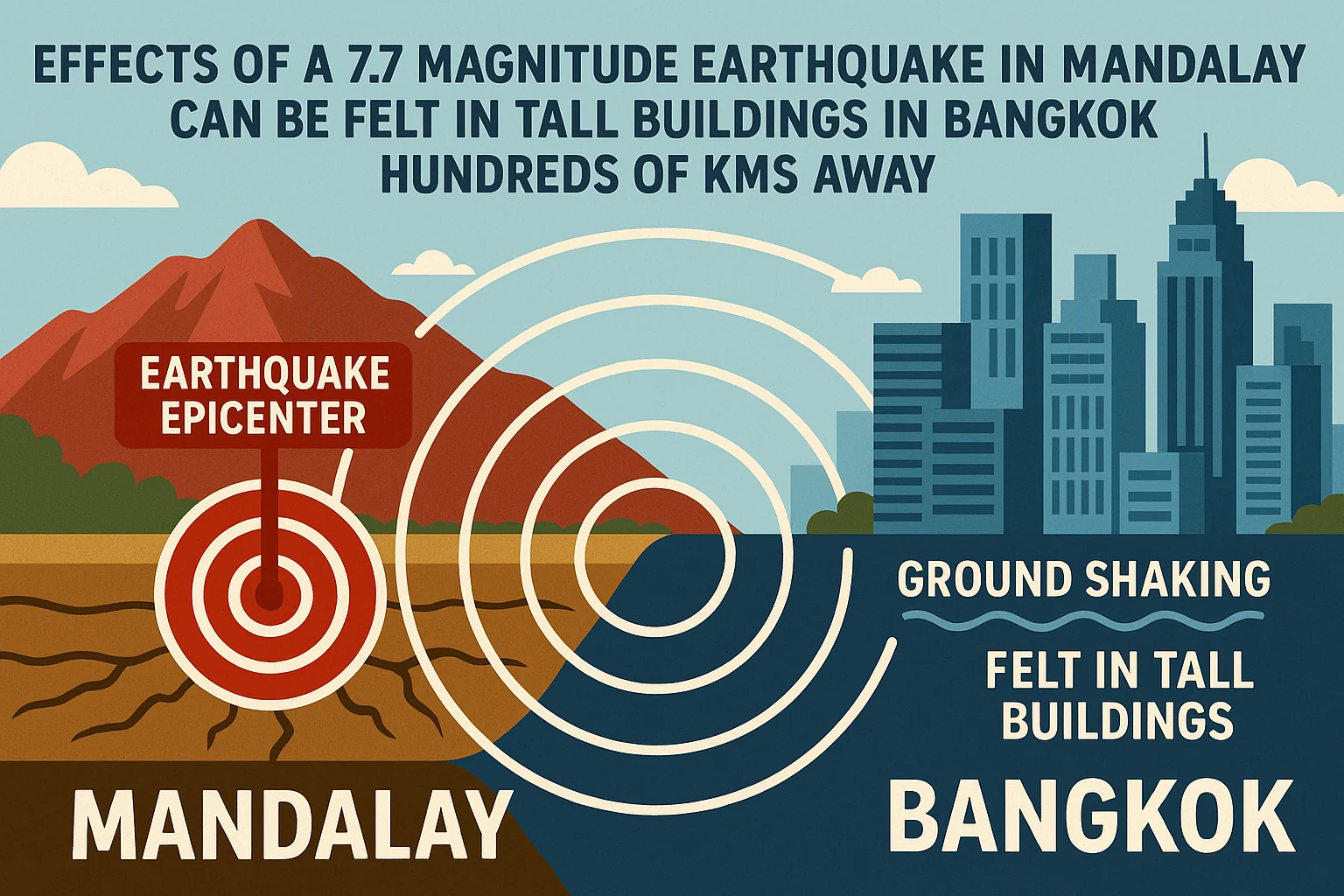
The earthquake was reported to have a magnitude of 7.7. Do you know what that means? The Richter scale uses common logarithms to make the measurements manageable (i.e., a magnitude 3 quake is a factor of 103 while a magnitude 5 quake is a factor of 105, meaning its seismometer readings are 100 times larger). In terms of energy released, each whole number increase on the Richter scale corresponds to an increase of roughly 32 times the amount of energy, and each increase of 0.2 corresponds to approximately a doubling of the energy.

The reason I mention this is that I think it's a worthwhile real-life example of exponential growth to discuss in a maths lesson.
Finally, the answer to last month's puzzle which was:
Addel Adgood, a hard-working student, has earned a number of trophies in the last month. She wants to share them among her three younger brothers, according to these fractions of the total:
At first glance, it seems impossible to divide the number of trophies she has exactly into halves, thirds, and eighths. Then, someone suggests 'borrowing' one extra trophy from a friend, temporarily increasing the number of trophies Addel has. Now the given fractions are possible and there will be one trophy left over, which can be returned to the friend.
How many trophies did Addel initially have?
The answer is 23
That accounts for all 23 of Addel’s trophies, and the borrowed trophy can be returned! Strangely, the numbers still match perfectly—yet each brother seems to have received at least the fraction he was due “out of 23.” Is this an astonishing solution, or just a clever piece of misdirection?
The first five people to respond with an answer to the puzzle were Kevin, Allan, Nick, Mala and Rick. Thanks to everyone who took part, I appreciate you getting involved. Some solutions can be seen below.
You can hear Rick's solution in this month's podcast. You can find it here, on Spotify or on Apple Podcasts. You can follow Transum on BlueSky, Twitter (some call it X) and 'like' Transum on Facebook.
That's all for now,
John
P.S. I want you to know that I, for one, like Roman numerals.
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Kevin, Queensland, Australia
Saturday, March 1, 2025
"In the puzzle we are looking for a number that can be divided by 2, 3 and 8. The smallest number with this property is 24. So Addel has earnt 23 trophies and borrows one.
One half of 24 is 12
One third of 24 is 8
One eighth of 24 is 3
Total is 23 so can return the 24th trophy after borrowing it.
Addel initially had 23 trophies "
Allan, Germany
Sunday, March 2, 2025
Mala, New Zealand
Tuesday, March 4, 2025
"Let x be the total number of trophies.
1/2 x + 1/3 x + 1/8 x = 23/24 x
which means she has at least one of them.
In total, there are 24 trophies of which the eldest brother gets 12, the middle one gets 8 and the youngest gets 3 (1 + 12 + 8 + 3 =24)."