Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of November 2022. It begins, as usual with the puzzle of the month.
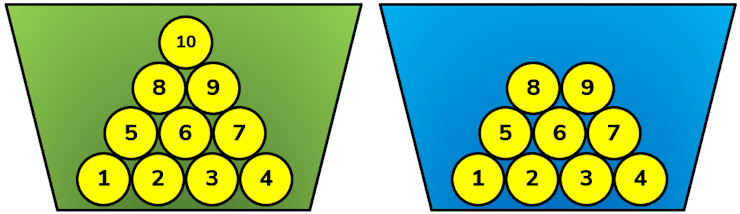
Randomly pick two different balls from the same pot then add the numbers on those balls together. The probability that this sum is odd is the same no matter which of the two pots you choose.
The puzzle is to figure out why this is true despite the fact that the green pot has an extra even number in it. Would it be the same if there were only eight balls in the pot?
This puzzle was inspired by Chris Smith's newsletter (Issue 609) and I have planned to make it an Advanced Starter but I don't yet have a simple, concise answer - that's is why I have posed it as this month's puzzle and I hope you are able to provide me with that insight.
While you think about that here are some of the key resources added to the Transum website during the last month.
The new Express Percentage Puzzle is intended as an extension exercise for those completing the Express as a Percentage online exercise. The interactive challenge comes in three levels. The puzzle level difficulty is inversely proportional to the difficulty of the percentages used!
The Subtraction Game is the name of a simplified version of the age-old and time-honoured game of Nim. The Transum version of Nim has been a very popular part of the Transum website for many years but now playing Nim is more accessible with the addition of this simplified version. Though it is called the Subtraction Game the winning strategy requires an understanding of multiples. Enough said?
A new level has been added to the Standard Form exercise. It is a nice task requiring learners to rewrite fractions containing standard form numbers in their denominators in correct standard form.
Have you seen one of these before?
It's called a Maths Monkey and I saw them on sale for £2.50 at a discount book shop. I thought I'd buy one and then try to figure out how it works. You move its legs to the two numbers you want to multiply together and the answer appears cupped in the monkey's hands. There is so much to wonder about!
When I was younger, November meant one thing and that was bonfire night. We looked forward so much to the fifth of November and lighting up the sky with the fireworks we had bought from the corner shop. You too can enjoy the November excitement in the classroom by using the Firewords starter, complete with sound effects.
Subscriber Ann has been doing some deep thinking inspired by a Transum interactive activity called the Tower of Hanoi. The story that goes with this activity is as follows:
Somewhere in India there is a temple which contains a large room with three old posts and 64 golden disks. Brahmin monks, acting out the command of an ancient prophecy, have been moving these disks for countless years. According to the legend, when the last move of the puzzle will be completed, the world will end!
I will let Ann continue:
"What’s the biggest problem when you’re playing the Tower of Hanoi? You lose concentration or get interrupted and can’t remember the direction of play.
Have you ever noticed that some pieces move more often than others? The smallest piece is constantly on the move. What about the largest piece? Have you noticed that it only makes one move in the entire game? It’s either on START or FINISH.
This is a game of two parts. In the first part, we’re trying to demolish the stack on START to free the largest piece. In the second part, the largest piece is now on FINISH and we are trying to build a stack above it.
When the monk goes to the Temple, the first thing he will ask himself is ‘Where is the largest piece?’
What does the monk ask himself next?
Ages ago, you asked me if there was an algorithm. I suppose there is. The monk only needs to ask himself five questions at most to know the next move.
It’s surprisingly easier to do than expected. I’m not great at the Tower of Hanoi, I lose concentration easily but I can do the Temple Challenge. Would you like to know the monks secret? It’s here."
Ann would love to hear if you have any comments after reading her instructions. She would also be very interested to know if the Tower of Hanoi actually exists. Has anyone seen it? Would anyone have photos? The temple is a religious place so it’s possible that there are no photos. On the other hand, there may be no photos because it’s only a myth.
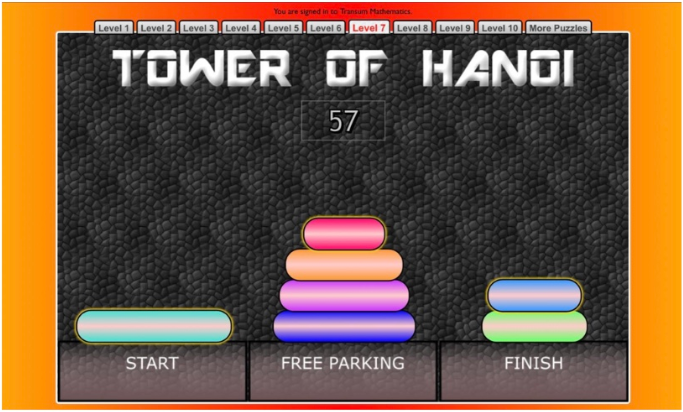
Which piece should you move next? Can you tell just by looking?
Finally the answer to last month's puzzle "Amir owes £100 to Beth. Beth owes £200 to Chris. Chris owes £300 to Dalbir. Dalbir owes £400 to Amir. What is the minimum amount of money that must change hands in order to settle these debts, and who should pay how much to whom?"
The best answer was provided by Wil:
"It looks to me as if overall A is owed 300, B, C, D each owe 100, so if B, C, D each pay 100 to A that will do it. Can't see anything simpler."
That's all for now,
John
P.S. f(x) walks into a bar. The barman says, 'Sorry, we don't cater for functions!'
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
