Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Glad tidings and festive felicitations! This is the Christmas edition of the Transum Newsletter and with it comes my best wishes for you and your families. It begins, as usual with the puzzle of the month.
I am looking at the ornaments hanging on the Christmas tree (which are all one of three colours) and I notice that:
How many ornaments are on the tree and how many of each colour are there?
While you think about that here is the latest Transum news:
Many of the activities on the website have been updated during November and, in preparation for the festive season, the ChristMaths collection has been brightly polished.
The first door of the Maths Advent Calendar is now unlocked!
Here are the three main additions to the ChristMaths collection:
Christmas Tree Light Up is an application I've purchased for the site because I think it is a great puzzle for this time of year. It is the perfect challenge for the student that doesn't give up easily and appreciates a task they can really get into. I've just been doing it in a coffee bar on my iPad and found it really engaging.
Countdown to Christmas is not to be confused with the Maths Advent Calendar or the Starter called Countdown. This brand new game is designed for two players though you can choose to have Santa (the computer) as your opponent if you have your heart set on winning a trophy. The unusual calendar shows the December dates leading up to Christmas and each player can select one, two or three dates each turn. The player to select Christmas Day wins. There is a guaranteed winning strategy which can be figured out by considering the numbers used in the game.
Systematic Snowflakes How do you make an old puzzle look new and fit for the festive season? Fill it with coloured snowflakes is the answer! A Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. This new yuletide activity is just a Latin square with snowflakes. Very pretty!
I was contacted by a boy named Michael from Australia a few weeks ago. He told me he had completed Times Square Level 1 in 9 seconds! I didn't believe him but he sent me a video as proof. I've added the video lower down the Times Square page and I'm sure you, like me, will be quite amazed.
A new Video has been made for the Listing Strategies activities. It was designed for students to watch excerpts of depending on the activity they are doing but it could be watched in its entirety if you pause it at suitable places while the students have a go at finding the answers to the questions asked.
A new level 6 has been added to the Coordinates exercise adding even more depth to the learning experience. By finding the coordinates of rectangles' vertices I think learners will have to think more about the numbers that make up coordinates rather than just corridors and stairs. So with the plotting, reading and coordinate pictures have I covered everything?
One less real-life opportunity for trigonometry exam question setters was in the news last month. True north, magnetic north and grid north are currently all the same in certain parts of the UK. It certainly makes old-fashioned map reading (on wet North Wales mountains circa 1975 for me) a lot easier!
Finally the answer to last month's puzzle which I have now made into an Advanced Starter:
Tree diagrams can be used to find the answers to (a) and (b).
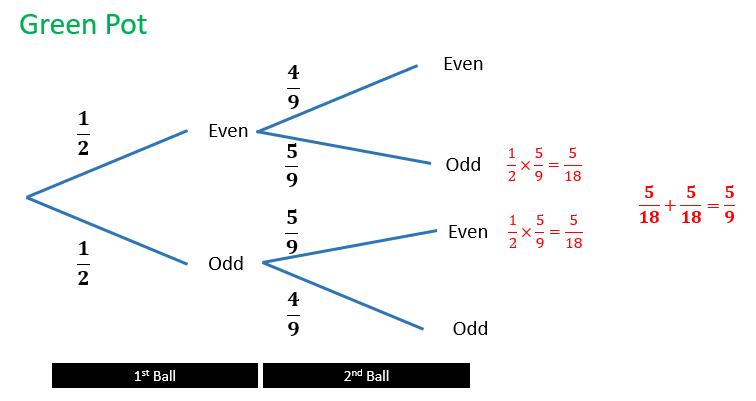
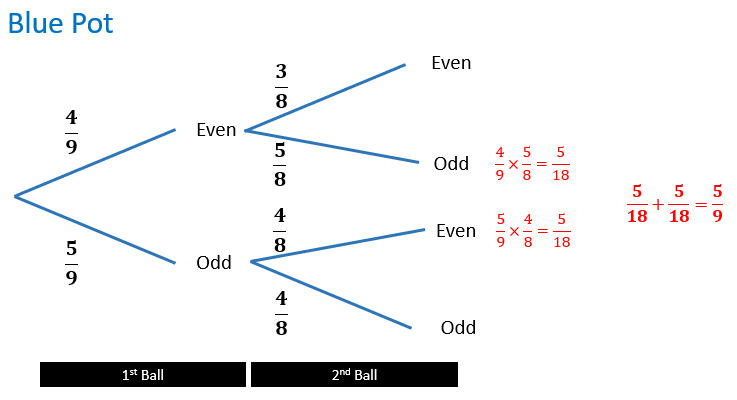
I would love to hear how students might account for the fact that the two probabilities are the same despite the different numbers of balls in each pot.
The result for eight balls in a pot is not the same (in case you were wondering).
Enjoy your Christmas break and I will be back in 2023,
John
P.S. Q. How is an artificial Christmas tree like the square root of minus nine?
A: Neither has real roots!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Rick, Podcast Listener
Saturday, December 31, 2022
"Regarding the probability puzzle in the November 2022 podcast, the solution can be generalized for pairs of values where the even number is one greater than the odd number (for example, 9 and 10, 99 and 100, 3 and 4, and so on). It will not work when the odd number is larger, like 8 and 9. Probabilities for a first and second draw are calculated and multiplied together to get the total probability. One needs to draw one even and one odd ball to create an odd sum. Using n to represent the even number, then the probabilities can be calculated as follows:
For the case of n balls, there is an equal number of odd and even balls present for the first draw. One will draw either an even number or an odd number on the first draw, so this probability is 1. The resulting probability for the second draw is:
P = (n / 2) / (n - 1)
We must calculate two probabilities for the odd numbered pot, since there are more odd numbers than even numbers. These probabilities will be added together for a total probability.
For the case where an odd number is drawn first, the probability of drawing an odd number on the first draw is:
P = (n / 2) / (n - 1)
After the first draw of an odd number, there are an equal number of odd and even balls, so the probability of getting an even ball on the second draw is one half, resulting in the first probability as:
P = (n / 2) / (n - 1) x (1 / 2)
For the second case, the probability of drawing an even ball first is:
P = (n / 2 - 1) / (n - 1)
And the second draw of an odd ball is:
P = (n / 2) / (n - 2)
Resulting in a final probability of:
P = (n / 2 - 1) / (n - 1) x (n / 2) / (n - 2)
Reducing terns:
P = (n / 2) / 2(n - 1)
Note that both these probabilities are the same, whether an odd or even ball is first drawn and they are one half of the probability when starting with an even number of balls in a pot. Adding these probabilities together results in the total probability of selecting an odd sum when starting with an odd number of balls and this probability is the same as when starting with an even number of balls."