Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Welcome one and all to this update. This is the Transum Newsletter for the month of August 2025. It begins, as usual with the puzzle of the month.
What number equals the mean of its digits?

Despite that being an 'average' puzzle it must be the shortest puzzle of the month ever! If you get an answer I’d love to hear how you or your students solved the puzzle. Let me know at: gro.musnarT@rettelsweN
While you think about that here are some of the key resources added to the Transum website during the last month.
Huge Numbers is a new resource designed to support teachers working with students on the Functional Skills learning objective: "Carry out calculations with numbers up to one million, including strategies to check answers such as estimation and approximation." It's essentially a curated collection of semi-randomised questions that require manual calculation methods, with a focus on accuracy. Did you know that most numbers are, in fact, huge?
Words and Concepts is a vocabulary exercise. A passage is provided with ten missing words, and students have to type in the correct words and spell them correctly too. The activity originally had only one level focused on algebraic words, but I’ve now added a second level featuring geometric terms.
Lobster Pots is a strategic risk-and-reward dice game in which players act as lobster fishermen, deciding each day where to place their pots, safely in the bay or at greater risk out at sea, in the hope of maximising profits over a fortnight while navigating unpredictable weather conditions.
This game is well known in UK schools and is used to reinforce mathematical skills such as probability, times tables, and decision theory. Despite its popularity and widespread use, no definitive origin or creator has been identified. Luckily, subscriber Jen stepped in with a version of the game she created and has very generously shared her resource with us all. Thanks Jen.
Tablesmaster Phone Edition is a new page.
I started creating the Transum website long before smartphones became as popular as they are today, so I optimised all of the activities to be viewed on a computer screen. Although the pages work really well on iPads, phone screens are just too small to clearly see what’s going on.
As Tablesmaster is so popular, I’ve now created a version specifically designed to be used on a smartphone. So, for all those students on the school bus who can’t think of anything else to do with their phone (as if!), they can always practise their times tables while travelling to and from school.
A lovely Advanced Starter on combinations and permutations has been created, called Safest Safe. It's one of those mathematical situations that seems to go against intuition. Suitable for a range of abilities when presented in different ways.
Another Advanced Starter has appeared. This one is called One Candle Each, and is a simple situation leading to what you might think is an unusual probability problem.
Both of these Starters were inspired by the book Headscratchers: The New Scientist Puzzle Book which is an excellent read. I highly recommend it and it is available online in a digital format - a plus for me.
Talking of books, when I was on holiday last week I found a book in my Kindle reader that I had no memory of downloading. It must have been recommended to me at some time in the past probably because maths problems were intertwined in the crime fiction. I'm sure you won't miss a beat solving puzzles such as "Water flows into a tank. The volume of water doubles every minute. The tank is full in one hour. How long does it take for the tank to be half full?" The book is called I’m Travelling Alone by Samuel Bjork translated into English from the original Norwegian.
Transum has an activity called Maths vs Math celebrating the different words used for mathematical concepts on either side of the Atlantic. With that in mind I enjoyed seeing this map posted in a discussion forum this week with the title "How Countries in Europe say Mathematics".
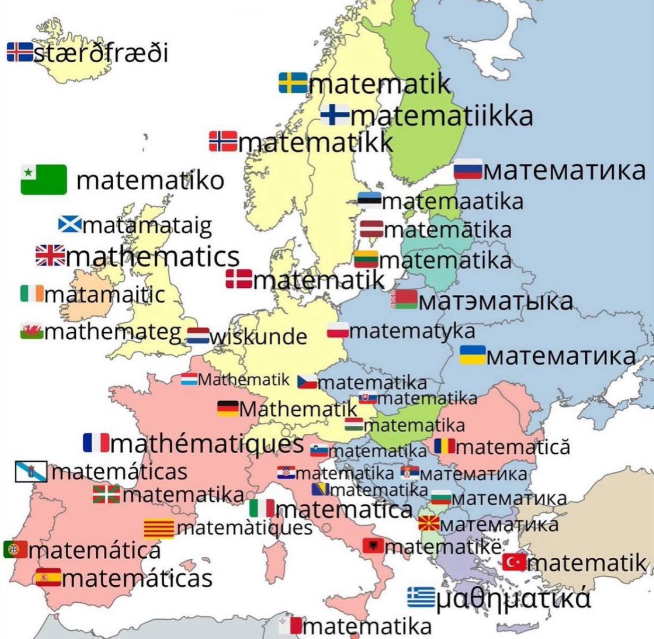
Posted on Reddit by user ImthebestGG (If you are the original creator or have additional details, please get in touch so proper credit can be added.)
Don't forget you can listen to this month's podcast which is the audio version of this newsletter.
Are your students on their long summer holiday at the moment (sorry southern hemisphere)? If so, recreational Maths activities not only reinforce academic concepts but also promote critical thinking, creativity, and a love for learning. So here's an idea: send your students an email containing a link to my collection of Holiday Maths Activities.
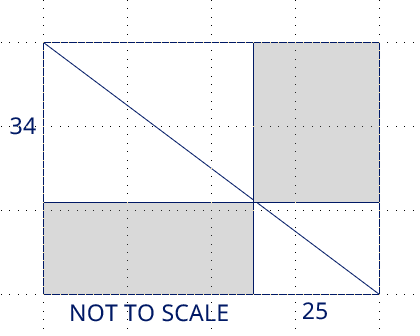
Finally the answer to last month's puzzle which was:
A rectangle is drawn inside a right-angled triangle. One vertex of the rectangle coincides with the triangle's right angle. Another of the rectangle's vertices meets the triangle's hypotenuse. The rectangle is 34mm from one of the acute angles and 25mm from the other. What is the area of the rectangle?
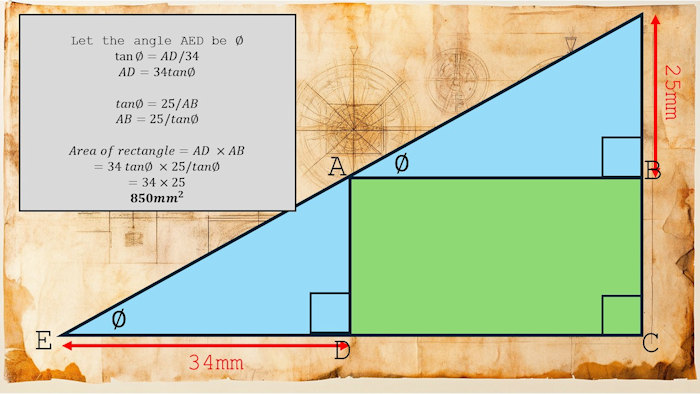
However, I like my method a lot less than I like the simplicity, efficiency and elegance of the methods shared in the comments below. Wonderful!
When I received the first solution from Chris I wrote back to him saying that I didn't think I'd receive any other correct solutions. Happily I was proved wrong. A huge thanks to all who took part ... now can you solve this month's puzzle?
That's all for now,
John
P.S. I'm in dispute with the numbers 1, 3, 5 and 7.
The odds are against me.
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Chris, Scotland
Tuesday, July 1, 2025
"Here’s my quick answer to your puzzle. I’ve just made porridge for 50 at our church summer camp and waiting for the team to wake up so had a couple of spare minutes!!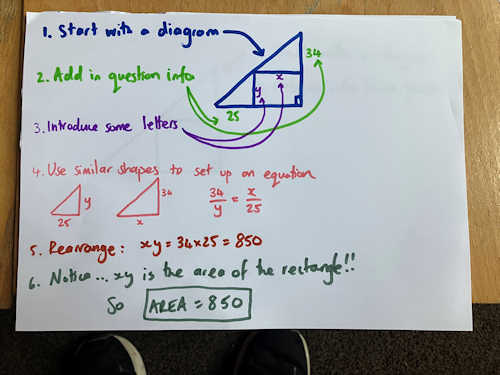 "
"
Leonard, USA
Wednesday, July 2, 2025
"After boring myself with similar triangles and a couple of Pythagorean approaches, I landed on this for my submission.
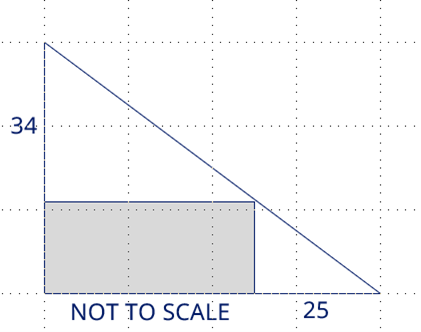
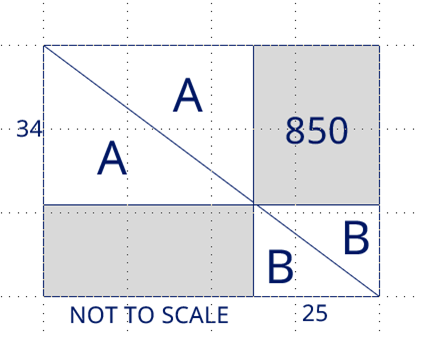 "
"
Starting with:
I extend the drawing to get:
With A=A and B=B by symmetry, the two shaded regions must also be equal. But the upper shaded region is simply 34 * 25 = 850, which is my answer.
Kevin, Australia
Thursday, July 3, 2025
"Let rectangle have length x, width y
From similar triangles 34/x = y/25
So area = xy = 34 x 25 = 850
😲 "
Rick, USA
Monday, July 7, 2025
"When I first listened to the July puzzle of the month, I was in bed ready for some shuteye. I drifted off to sleep thinking about trying to solve for the length of the rectangle sides using the Pythagoreans theorem. I was soon asleep but when I woke up, I realized this was not the correct approach.
Next, I considered an isosceles right triangle. In this case, the sides of the rectangle are 34 and 25 mm, since those are the lengths of one of the sides of each of the smaller triangles formed when drawing the rectangle, leading to an area of 34 x 25, or 850 square mm. Since the puzzle called for a specific answer, one could assume that if this is the area for a specific triangle, it would be the same for others and leave it at that. But I figured that I should look for a general solution for all triangles, using formulas for the area of a triangle and rectangle.
Using the following variables:
Height of rectangle = h
Width of rectangle = w
34 mm = x
25 mm = y
Then, the area of the right triangle is:
((h+x)(w+y))/2, or
(hw+hy+xw+xy)/2
The triangle area can also be expressed as the area of the rectangle plus the area of the two smaller triangles:
hw+(xw)/2+(hy)/2
Equating the two areas:
(hw+hy+xw+xy)/2=hw+(xw)/2+(hy)/2
Multiplying both sides by 2:
hw+hy+xw+xy=2hw+xw+hy
Subtracting hw+hy+xw from both sides:
Xy=hw
Since hw represents the area of the rectangle, this area is also xy, or substituting the actual lengths for x and y, 34 * 25, or 850 square mm. "
Stephen, England
Wednesday, July 9, 2025
"Love this month's puzzle.
I used similar triangles to put x/34 = 25/y
(where x and y are the dimensions of the rectangle)
From there, xy=25*34=850 sq mm
Great puzzle! 👏"
Mala, New Zealand
Sunday, July 13, 2025
"The answer to this puzzle:
Let one of the acute angles be called A. Let x and y be the lengths of the sides of the rectangle.
Since corresponding angles on parallel lines are equal,
y/34 = tan A
25/x =tan A which implies that y/34 = 25/x
Therefore, the area of the rectangle = xy = 850 square mm.
✅"
Páraic, Irishman in Paris
Thursday, July 31, 2025
"Having written several pages of algebra, and torn them up one by one, I decided the best approach was pure geometry. I drew a simple diagram of the triangle with the rectangle inscribed within it
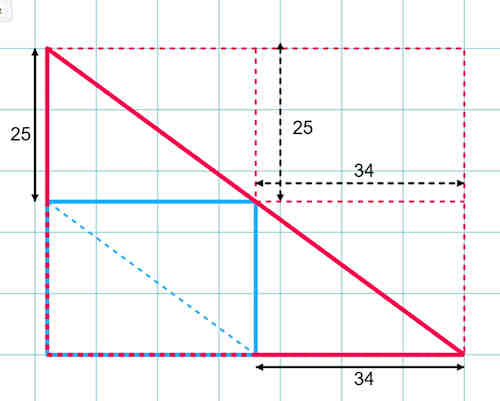
That shows that each side of the rectangle must be the same length as the distance between it and the corresponding apex.
Therefore the rectangle is 25×34 = 850
Thank you very much for these interesting puzzles! "