Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Transum Newsletter for the month of September 2025. For a change, this month’s Puzzle of the Month is adapted from an 1885 school textbook. If you get stuck, you could always ask your great-great-great-great-grandparents for help!
Farmers A and B have 30 cows between them and sell at different prices; each receives the same amount. If A had sold at B’s price, he would have received £320, and if B had sold at A’s price, she would have received £245. How many cows did Farmer A own?

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Fire off an email to: gro.musnarT@rettelsweN
While you think about that, here are some of the key resources added to the Transum website during the last month.
Transformation Golf is now available on the website. It offers a focused way for students to practise transformations on a coordinate grid, choosing and deciding on values for translations, rotations and reflections to land a point on a target. The nine-hole structure introduces progressively tighter constraints, encouraging careful selection of vectors, centres and angles, and promoting efficiency through a visible scorecard. There are lots of other versions of Transformation Golf on the internet, but I hope you'll see this one is a little different to the rest and focuses on students thinking deeply about transformations.
Arguable Area is a new Advanced Starter and looks like this:
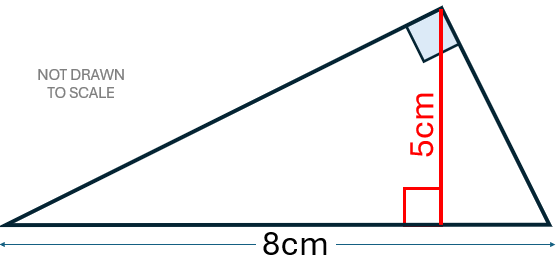
Find reasons why the area of this large right-angled triangle might not be 20 cm2
I am guessing that most students won't realise that the triangle with the given dimensions is impossible (most of us teachers wouldn't notice it either). Nevertheless, this starter is worthwhile because it will get the students to think about geometric properties, conventional diagrams, rounding, accuracy and possibly many other things in attempting to come to a solution.
Primes and Squares is a collection, like a mixtape or playlist, of online activities designed to deepen understanding of prime numbers and square numbers. It has been created for Thursday, 4 September 2025, when the date, in short form (4/9/25), will be the squares of the first three prime numbers. Unique!
If, however, you favour the (less logical) month/day/year date format you have the squares of three, four and five to look forward to on 9/16/25. Also Unique!
(Stop press: Just found out that all of the digits of the 27th of this month are a very large square numbers regardless of the order of the month and the day! 27092025 and 9272025.)
Treasure Hunt is a place where teachers can generate a set of ten clues for a fun activity. Just choose ten locations around your school grounds that are accessible to pupils and the magic of this web page will do the rest. You could call it a Treasure Hunt Clue Generator.
Mental Maze is a new number-path challenge in which pupils start with a given value and navigate adjacent operation tiles to reach a stated target. It promotes clear mental methods, estimation and checking with inverses. Difficulty can be adjusted (though Level 1 is going to provide challenge enough for many), with an optional subscriber-only reveal of the solution path.
As this is the September Newsletter, I thought a reminder of the Back To School page was in order. I summoned up the power of my genie (AI) to create some images for this Newsletter which you can see below. I'm sorry if the teacher in the images doesn't look like you, and your pupils aren't quite as keen and neatly turned out!
Interesting dates for the coming month:
1st September :: First day of the last third of the year.
4th September :: The date numbers (short form, day first) are the squares of the first three primes.
16th September :: The date numbers (short form, month first) are the squares of three to five.
19th September :: Talk Like a Pirate Day :: Numbers in Words Challenge.
27th September :: The date digits (either form) form large square numbers (see above).
Don't forget you can listen to this month's podcast, which is the audio version of this newsletter. You can find it here and on all good podcast platforms. Search for Transum Mathematics Puzzles.
Due to persistent automated attacks by malicious bots, the following applications are now restricted to Transum subscribers: Compound Interest Calculator, Triangle Solver, Normal Distribution Calculator, Tree Diagram Creator and the Student Voting System. I am sorry for any inconvenience; it is a pity that so much time must be spent protecting the site rather than building new features.
Finally, the answer to last month's puzzle, which was:
What number equals the mean of its digits?
This puzzle is adapted from Alex Bellos's Monday puzzle column in The Guardian (14th April 2025)
The most worthy solution 4.5
If you allow trailing zeros, there are many more. For example: 1.500, 2.250, 3.750, 1.8000 and 0.200000000. In addition, there are some more ideas in the comments below. Thanks to all of you who took part and sent me solutions. Fabulous!
Finally, here is a contentious solution that popped into my head in the middle of the night: eight point nine recurring.
That's all for now,
John
P.S.
Teacher: "How many times can you subtract 7 from 83, and what is left afterwards?"
Student: "I can subtract it as many times as I want, and it leaves 76 every time!"
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.
Chris, Scotland
Friday, August 1, 2025
"First, there are one digit numbers whose digits are, by definition, the mean of their digits… so -9,-8,-7,….7,8,9.
Two digit numbers have a mean at most 9 so that’s a dead end.
We’re going to have to hunt for decimals if we’re to uncover further answers…
If they’re two digits:
4.5 does the business (9/2=4.5)
The only other ones I’ve come up with have a fixed number of declared zeroes at the end like:
1.500 = 6/4
2.250 = 9/4
3.750 = 15/4
1.8000 = 9/5
1.1250000 = 9/8
1.687500000000000 = 27/16
Those seem like cheating as obviously there are more zeroes following the zeroes I’ve stuck on the end. And maybe your readers will uncover more!
Thanks for a fun puzzle! I enjoyed finding solutions "
Mala, New Zealand
Saturday, August 2, 2025
"I think the only answer to this is the number 4.5 as it is equal to the mean of 4 and 5 (which is 9/2 or 4.5).
 "
"
Leonard, United States
Saturday, August 2, 2025
"Here’s what I have so far.
Obviously, all ten single digits work: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. In these cases, the number also equals the median and mode of its digits.
I believe the standard answer is: 4.5 = (4 + 5) / 2 .
How about: 20 = 1 = (2 + 0) / 2, or 1! = 1, or 2! = 2.
Also: 1 / 0.5 = 2 = (1 + 0 + 5) / 3 .
10 / 5 = 2 = (1 + 0 + 5) / 3 . This one “pairs” with 1 / 0.5.
24 / 6 = 4 = (2 + 4 + 6) / 3
35 / 7 = 5 = (3 + 5 + 7) / 3
54 / 9 = 18 / 3 = (5 + 4 + 9) / 3
Or, stretching the rules a bit: 2.250 = (2 + 2 + 5 + 0) / 4 = 2.25, and 3.750 = (3 + 7 + 5 + 0) / 4 = 3.75 .
And, if you bought those: 0.500000000 = (0 + 5 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0) / 10 = 0.5 .
Still working on this great puzzle. I might be at it all month.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
My final (not complete) set of fractions.
36/12, 56/14, 81/18, 65/20, 63/21, 92/23, 90/24, 90/30
126/42, 162/45, 288/48, 153/51, 286/55, 232/58, 180/60, 288/60
396/66, 315/75, 304/76, 340/85, 493/85, 324/90, 486/90, 558/93
I’m thinking that 8.9 repeating is more of a philosophy question than a mathematical one. I need to review some sequence and series topics I’m sure I knew at one point. "
Rick, United States
Friday, August 8, 2025
"I have had what I perceive is the desired answer to the august 2025 for several days but wanted to explore other possibilities. However, this is taking longer than I planned, so I am sending you my solution before I forget. Hopefully, I will have an update later this month.
What number equals the mean of its digits?
The mean of a set of numbers is calculated as:
Mean=Sum of all numbers/Number of elements
However, the mean is valid for a single number.
So, if the set contains only one number, say, x, then:
Mean=x/1 or x
In this case, the mean is simply the number itself. This is mathematically consistent and valid,
Hence, the numbers 0 through 9 satisfy the solution to the problem.
However, I doubt this was the desired solution, so I looked at alternatives.
Since the mean consists of a set of numbers in the range of 0 to 9, the mean has to be a number in the range from 0 to 9. Therefore, we can eliminate any numbers greater than 9. The only way to get more digits is to look at fractional or decimal numbers. I first considered fractional numbers. I found a couple of solutions, none extremely interesting, but I include them here for completeness:
1 - 0/2, which is equal to 1 and so is its mean.
2 – 04, which is equal to 2 and so is its mean.
Hopefully, I can find more interesting fractions. This may require some Python scripting.
Finally, I decided to investigate decimal numbers. Obviously, 0.0, 0.00, 0.000 , and so on satisfy the solution space. But I had a feeling this still was not the intended answer.
To search for what I perceive was the desired solution, I initially considered decimal numbers with only one number following the decimal place (a number consisting of only two digits). that the resulting mean of a number with only two digits would either be a whole number or a number with five in the decimal place. Since the value of the mean of two digits which add up to an even number would result in a whole number value, we only need to consider numbers like 2.0, 4.0, 6.0, and 8.0. But none of these satisfy the solution space, since their mean is half their value. We need to consider the numbers 2.5, 4.5, 6.5 and 8.5, of only which 4.5 satisfies the requirement that the mean is equal to the number.
So, I submit that 4.5 is the intended solution to the August 2025 puzzle of the month. "