Mathematical Investigation

STRANGE SNOOKER

Level 1 Level 2 Level 3 More Investigations

Bounces Pocket

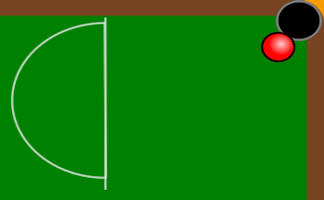
Click the snooker cue to begin.

Choose a different width and height to see what difference that makes.

This is a very strange snooker table. It has only has four pockets and the ball always travels at an angle of 45° to the sides of the table.

Given the width and height of a table can you predict which pocket the ball will end up in and how many times will it bounce off one of the sides?

Collect some data for different sized snooker tables. You may wish to collect your results in a spreadsheet so that you can investigate the relationships between the numbers.

Note that the number 6 is missing from the drop-down selectors. That is because the 6 is being saved for level 2.

If you use the table below to collect your data you can earn a Transum virtual trophy for finding ten different cases.

  Width Height Bounces Pocket  
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃
  ✔ ❌ 🔃

Check

🔃 This symbol will appear next to a row that is a duplicate of a previous row. If you see this symbol or the cross which indicates incorrect figures, you can make corrections then click the Check Again button.

In addition to the number of bounces and the destination pocket you could also investigate how far the ball travels before falling into a pocket? Using a spreadsheet may help manage the data you collect. There are many things you could.

If you like snooker you may be interested in playing the Snooker Angles game:

Transum.org/go/?to=snookerangles

Student Activity

Investigations Home

Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.

A mathematical investigation is quite different to other mathematical activities. The best investigations are open ended and allow students to choose the way they work and how they record their findings. It is one of the few occasions when 'going off on a tangent' is not only acceptable but actively encouraged (within reason).

Students may ask for 'the answers' but this supposes that the activity is closed. Investigations can always be extended by varying the initial instructions or asking the question 'what if...?'. Sometimes students point out that the instructions are ambiguous and can be interpreted in different ways. This is fine and the students are encouraged to explain how they interpreted the instructions in their report.

Some students may benefit from a writing frame when producing the reports of their investigations. Teachers may suggest sections or headings such as Introduction, Interpretation, Research, Working and Conclusion or something similar.

Here are some other activities you may be interested in:

Featured Activity

Practice Papers

Practice Papers

Mathematics GCSE(9-1) Higher style questions and worked solutions presented as twenty short, free, practice papers to print out.
Suggested

Remainder Race

Remainder Race

A game involving chance and choice requiring an ability to calculate the remainder when a two digit number is divided by a single digit number.

The short web address is:

Transum.org/go/?to=remainder
Recently Updated

Shape Sorter

Shape Sorter

Drag each shape into the correct bin according to their types and symmetries. So far this activity has been accessed 204 times and 96 Transum Trophies have been awarded for completing it.

Teacher's notes for this investigation and solutions to Transum puzzles, exercises and activities are available when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher, tutor or parent you can apply for one by completing the form on the Sign Up page.

A Transum subscription also gives you access to the 'Class Admin' student management system, downloadable worksheets, many more teaching resources and opens up ad-free access to the Transum website for you and your pupils.

For Students:

 

For Teachers:

For All:

Transum.org is a proud supporter of the kidSAFE Seal Program
©1997-2024 WWW.TRANSUM.ORG

Though adapted and redesigned quite extensively, this investigation is based on Loopy Snooker created by D.Keith at www.subtangent.com and originally written in Flash.