Level 1 Level 2 Level 3 More Investigations
Width: Height: Speed:
Bounces Pocket
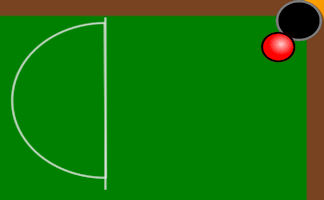
Click the snooker cue to begin.
Choose a different width and height to see what difference that makes.
This is a very strange snooker table. It has only has four pockets and the ball always travels at an angle of 45° to the sides of the table.
Given the width and height of a table can you predict which pocket the ball will end up in and how many times will it bounce off one of the sides?
You may have noticed that the number 6 was missing from the drop-down selectors provided in level 1. This level requires you to work out some results for either a width or length 6 for yourself.
You can do the work for this level on squared paper pr you could use the drawing aid above. Click the red circles (which represent possible bounce points) in order to daw a line to that point. Your diagram can show the path of the ball making it easier for you to count the number of bounces.
If you use the table below to collect your data you can earn a Transum virtual trophy for finding ten different cases.
🔃 This symbol will appear next to a row that is a duplicate of a previous row. If you see this symbol or the cross which indicates incorrect figures, you can make corrections then click the Check Again button.
In addition to the number of bounces and the destination pocket you could also investigate how far the ball travels before falling into a pocket? Using a spreadsheet may help manage the data you collect. There are many things you could.
If you like snooker you may be interested in playing the Snooker Angles game: