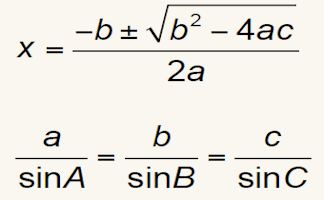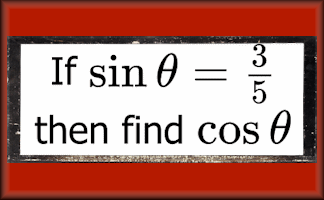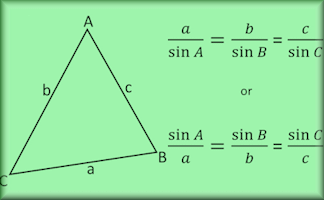There are 366 different Starters of The Day, many to
choose from. You will find below some starters on the topic of Trigonometry. A lesson starter does not have to be on the same
topic as the main part of the lesson or the topic of the previous lesson. It is
often very useful to revise or explore other concepts by using a starter based on a
totally different area of Mathematics.
Main Page
Trigonometry Starters:

It is called Refreshing Revision because every time you refresh the page you get different revision questions.
Advanced Trigonometry Starters
Exercises

3D Trigonometry Presentation
A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.
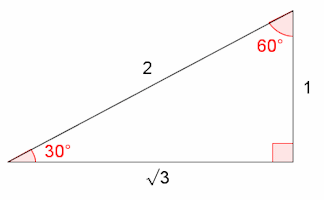
Common Trig Ratios Degrees
A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles.
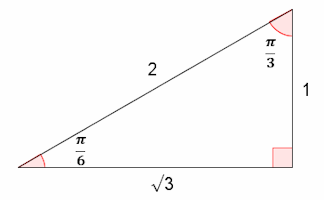
Common Trig Ratios Radians
A self-marking exercise on finding the exact values of sine, cosine and tangent of special angles given in radians.
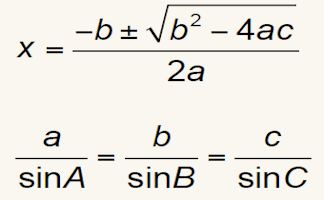
Formulae to Remember
The traditional pairs or pelmanism game adapted to test recognition for formulae required to be memorised for GCSE exams.
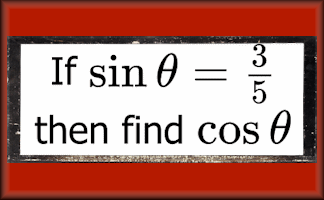
If Then Trigonometry
Finding the exact values of sine, cosine and tangent of angles if given a different trig ratio.
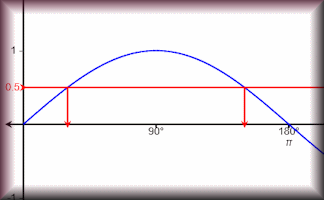
Inverse Trig Calculator
This calculator is designed to find all of the angles for a given trigonometric ratio and show them on a graph.
Triangle Solver
Provide and three measurements for a triangle and this application will work out the remaining sides, angles and area.
Trig Tour
See angles, in either degrees or radians, on the unit circle and the graph of the trigonometric function.
Trig-Pythag Fusion
Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem
Trigonometry
Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
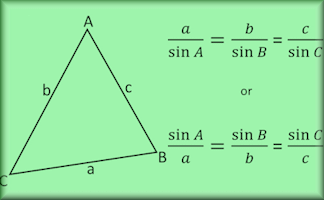
Trigonometry Advanced
A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
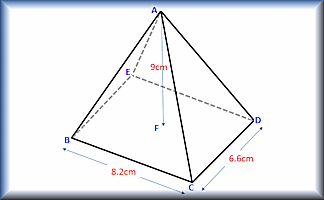
Trigonometry in 3D
Calculate the lengths of sides and the size of angles in three dimensional shapes.
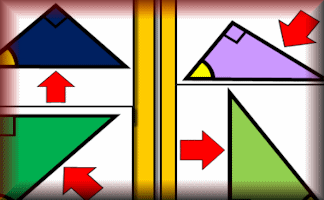
Which Side?
Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse.
Other activities for this topic | | |
Complete Index of Starters
Search
The activity you are looking for may have been classified in a different way from the way you were expecting. You can search the whole of Transum Maths by using the box below.
Have today's Starter of the Day as your default homepage. Copy the URL below then select
Tools > Internet Options (Internet Explorer) then paste the URL into the homepage field.
Set as your homepage (if you are using Internet Explorer)
Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world.
Click here to enter your comments.