

Find the first three terms in the expansion of:
\((3a - 2b)^9\)
\(=19683a^9 - 118098a^8b \\+314928a^7b^2 ...\)
If £180 is invested with an interest rate of 2% compounded monthly, find the value of the investment after 6 years. £202.93
Here are the coordinates of 3 vertices of a square, what are the coordinates of the 4th?
\((5,3),(8,9),(-1,6)\)
(2,12)
\( X \sim N(9.03, 0.89^2)\)
Find
\( P(7.15\lt X \lt9.01) \)
\(0.474\)
Factorise:
\(x^2-x-12\)
\((x+3)(x-4)\)
Factorise:
\(8x^2+10x-3\)
\((2x+3)(4x-1)\)
Draw a rough sketch of the graph of:
\(2y=x+4\)
Gradient 0.5
y intercept 2
What is the value of:
\(27^{\frac{1}{3}}\)
\(= 3\)
Find angle BCA if AC = 5.1m and BC = 7.1m. 44.1o
Find BC if angle BCA = 44o and AC = 6m. 8.34m
Describe the red region.


\(y = 5x^3 - 7x^2 + 3x\)
Find \( \dfrac{dy}{dx}\)
\(15x^2 - 14x + 3\)
\(y = \dfrac{3}{x^6} - 5\sqrt[6]{x}\)
Find \( \frac{dy}{dx}\)
\(-\frac{18}{x^7} - \frac{5}{6}x^{-\frac{5}{6}}\)
\(y=(7x^2-5)^5\)
Find \( \dfrac{dy}{dx}\)
\(70x(7x^2-5)^4\)
\(y=x^8 \sin x\)
Find \( \dfrac{dy}{dx}\)
\(8x^7sinx+x^8cosx\)
\(y=\frac{x}{\sin x}\)
Find \( \dfrac{dy}{dx}\)
\(\frac{(sinx-xcosx)}{sin^2x}\)
Find the equation of the tangent to the curve:
\(y = 4x^2 + 2x - 1\)
where \(x = -2\)
\(y = -14x - 17\)
Find the equation of the normal to the curve:
\(y = 3x^2 - 6x + 9\)
where \(x = 2\)
\(y = 9\frac{1}{3} - \frac{x}{6}\)
\(y =9x^2 - 16x + 3\)
Find \( \int y \quad dx\)
\(3x^3 - 8x^2 + 3x+c\)
A game is played 18 times and the probability of winning is 0.8. Calculate the probability of winning exactly 2 times. 0.000000000642
Make up a maths question using this:
\(\log_ax=\dfrac{\log_bx}{\log_ba}\)
Logarithm changing base formula
What letter is this?
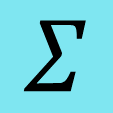

Two terms of an arithmetic sequence:
\(u_{5} = -12\)
\(u_{11} = -18\)
Find the sum of the first 28 terms.-602
Find the equations of the asymptotes of:
\(y=\dfrac{10-2x}{10x}\)
\(x=0,y=-{1}{5}\)
In the triangle ABC,
BC = 6.3cm.
CA = 10.1cm.
BĈA = 47.8°
Find AB to 1 dp.
7.5cm
Evaluate:
$$\sum_{n=3}^{6} 2^n$$
120
\(f(x)=3x^2+6x+6\)
What is the value of the discriminant and what does it indicate?
-36, No real roots
\(f(x)=x^2+8x-5\)
By completing the square find the coordinates of the vertex.
(-4, -21)
Solve for x:
\(\log_3x = 2\)
9
Find the integral:
\(\int \sin(x)\cos^2(x) \;dx\)
\(-\frac{1}{3} \cos^3(x)+c\)
Find the equation of the straight line that passes through:
(-2, 6) and (4, -6)
\(y=-2x+2\)
Find the inverse of the function \(f\):
\(f(x)=\frac{\sqrt{x-9}}{8}\)
\(64x²+9\)
\(\text{Find }f(x) \text{ if} \\ ff(2a-3)=\\18a-27 \\\)
\(f(x)=3x\)
Write in standard form:
\(a \times 10^p \times b\times 10^q\)
where \(a \times b \) is a two digit number \((10 \le ab \lt 100)\)
\(\frac{ab}{10}\times10^{p+q+1}\)
Draw a rough sketch of
\(x=\pm \sqrt{y}\)
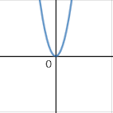
Sketch a height-time graph as this jar is filled.


Without a calculator find the exact value of
$$\cos{\frac{\pi}{6}} \times \cos{60°}$$\(\dfrac{\sqrt{3}}{4}\)
Without a calculator find the exact value of
$$\tan{\dfrac{19\pi}{3}}$$\(\sqrt{3}\)
Solve:
\( 5a+2b+c=31 \\ 3a+4b+2c= 41 \\ a+5b+c=34\)
a = 3, b = 5, c = 6
Find the perimeter of a sector with radius 5.2cm and angle \( \frac{\pi}{4}\)
🍕
14.5cm
A safe has a eight-digit code. How many possibilities are there if no digit can be repeated and the code must be odd?
907200
Find the equations of the asymptotes of:
$$y=\dfrac{-6x^2+5x}{2x+1}$$x=-1/2,y=4-3x
Evaluate:
$$ \sum_{k=1}^{15} 5 \times (-2)^k $$
-109230
Find the first 4 terms in the expansion of:
\(\dfrac{1}{(1+3x)^3}\)
\(1-9x+54x^2-270x^3\)
Evaluate:
\(\int^{120}_{60} \dfrac{1}{x} dx\)
\(\ln{2} \approx 0.693\)
Tin A contains 5 red balls and 8 green balls. Tin B contains 9 red balls and 10 green balls. A dice is thrown and if the score is less than 3 a ball is selected from tin A; otherwise a ball is selected from tin B. Given that the ball selected was red, calculate the probability that it came from tin B.
\(\frac{234}{329}\)
There are eight different ways that three planes can relate in three dimensions. One is where they all intersect at a point. How many of the other seven ways can you sketch or describe?
Simplify
$$ \dfrac{i(2-i)}{3-2i}$$
\(-\frac{1}{13}+\frac{8}{13}i\)
Evaluate:
\(\int x\tan^{-1}x\; dx\)
\((\frac{x^2+1}{2})tan^{-1}x-\frac{x}{2}+c\)
Simplify:
$$5\sin{x}+3\cos{x}\tan{x}$$\(8\sin{x}\)
$$ \DeclareMathOperator{cosec}{cosec} $$Find the volume of revolution when \(y=x(4-x)\) is rotated about the x-axis for \(0 \le x \le 4\)
\(\frac{512\pi}{15}\) cubic units
How do you use the discriminant to determine the nature of roots?
Clue: positive, negative or zero: \( b^2 - 4ac \)
Show how the first four terms of the Maclaurin series are obtained for
\(f(x) = \sec(x)\)
\(1 + \frac{x^2}{2} + \frac{5x^4}{24} + \frac{61x^6}{720}\)
Find the five 5th roots of 1
\(1, cis\frac{2\pi}{5}, cis\frac{4\pi}{5},\\ cis\frac{-2\pi}{5}, cis\frac{-4\pi}{5}\)
A school committee of 8 is chosen at random from 12 senior students and 4 junior students. Find the probability that all four junior students are chosen.
1/26 or 3.85%
Prove by mathematical induction that the sum of the first \( n \) even numbers is \( n(n + 1) \)
Show true for n=1, assume true for n=k, prove for n=k+1
Simplify
\(4\sqrt{7} - \sqrt{63}\)
\(\sqrt{7}\)
Write down a summary of your last Maths lesson focussing on what you learnt.
?
Tick (or untick) the boxes above to select the concepts you want to be included in this Starter [untick all]. The display at the top of this page will change instantly to show your choices. You can also drag the panels above so that the questions are ordered to meet your needs.
* Topics shown with an asterix are on the IB Higher Level syllabus but not included in the Standard Level syllabus.
This Starter is called Refreshing Revision because every time you refresh the page you get different revision questions.
Regularly use this Starter to keep that important learning from being forgotten. Here is the web address (URL) for the version of this page with your currently selected concepts:
Copy and paste the URL above into your lesson plan or scheme of work.
For more ideas on revision there are plenty of tips, suggestions and links on the Mathematics Revision page.
Answers appear here for Transum subscribers.
Try this Uniqueness Game with your class.
Transum.org/Maths/Game/Uniqueness/Game.asp?Level=8

Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Teacher:
Scroll down the
page to see how
this Starter can be customised so that it
is just right for
your class.