Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
How do you convert a fraction or decimal fraction to a percentage?
There's an error that keeps appearing in maths textbooks and online. I want to lead you there by posing a puzzle.
Oh really? I wasn't aware of that. I'm intrigued to hear your puzzle!
How do you convert a fraction to a percentage ? Most will tell me that's easy, I did this at primary school. You multiply by 100 and put a % sign on your answer.
Me: Like this ?
2/5 x 100 = 40%
Yes, they tell me.
Me: But that's not right.
Yes, it is. 2/5 is equal to 40%.
Me: It's right that 2/5 is equal to 40%. It's wrong that 2/5 x 100 = 40%
They might tell me that they're confused.
Can you spot what's wrong ?
We all agree that 2/5 is equal to 40%. It's all about how we get there.
2/5 = 2/5 x 1
2/5 = 2/5 x 20/20
2/5 = 40/100 = 40%
Yes you tell me.
So far we all agree.
Me: Now I'm going to use your method. I'm going to multiply by 100, like you told me.
2/5 x 100 = 2/5 x 100/1
2/5 x 100 = 200/5
2/5 x 100 = 40
Is that right ?
Yes, you tell me.
I keep writing....
40 = 40 x 1
40 = 40 x 100/100
40 = 4000/100 = 4000%
You scratch your head. Something has gone wrong.
I need your help. This is a widespread problem. It's in school textbooks, it's online, it's everywhere.
To convert a fraction to a percentage we have to multiply by 100%. That percentage sign is vital.
2/5 x 100% = 2/5 x 100/100 = 200/500 = 40/100 = 40%
Someone has been stealing our percentage signs.
Why do i care ?
A child asked me:
If I convert 2/5 into an equivalent fraction, I multiply by one don't I ?
Yes I said.
so, I can multiply 2/5 by 20/20 to get 40/100 which is 40% ?
Yes, I said.
then they asked: but if I use the formula to convert a fraction to a percentage I have to multiply by 100. Why don't we multiply by the same amount ?
I scratched my head.
Clever child.
I'm going to call it the Mystery of the Missing Percentage Sign. Someone has been stealing our percentage signs.
Yes agree that It's wrong that 2/5 x 100 = 40% when written as an equation. But if written as a process with function machines it seems to be OK:
I don’t think to convert a fraction to a percentage we have to multiply by 100% though. Here are my examples to show why that is wrong:
Which is not the percentage we want.
Which is not the percentage we want.
Which is not the percentage we want.
We all agree with this statement:
0.35 = 35/100 = 35%
Each of these statements below are correct because we are effectively multiplying by one in each case:
0.35 = 0.35 x 1
0.35 = 0.35 x 100/100
0.35 = 0.35 x 100%
If you have 100 percent of 0.35 then you have all of 0.35 which means that you have 0.35
I would mark all of your examples in the yellow boxes as correct.
I go back to the original question from the child:
Why do we multiply by one when we convert equivalent fractions BUT we multiply by 100 when we use the formula to convert fractions to percentages ? Shouldn't we be multiplying by the same amount ?
How would we answer that question ?
I'd say that we should be multiplying by the same amount. We should convert fractions to percentages by multiplying by 100%.
2/5 x 20/20 = 40/100 = 40% (multiplying by 20/20 is the same as multiplying by one)
2/5 x 100/100 = 200/500 = 40/100 = 40% (multiplying by 100/100 is the same as multiplying by one)
For the same reason, we should multiply decimals by 100% when we convert decimals to percentages.
Still not convinced about the percentage debate. To use your example:
0.25 = 0.25 x 100% (because 100 percent of 0.25 is all of 0.25 which is 0.25)
= 25%
My issue is the calculation you have done gives you the answer I have highlighted in yellow. You have then had to multiply that number by 100 in your head to get the answer I have highlighted in green. So I think you have actually multiplied by 100 as well as 100% (which has no effect as it is the multiplication identity).
Can I have one last go at convincing you ?
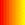
Have a look at these bar models.
If I have one pink box, I will have 1 x 0.5 = 0.5 (this is the same as 50%)
If I have two pink boxes, I will have 2 x 0.5 = 1.0 (this is the same as 100%)
If I have one hundred pink boxes, I will have 100 x 0.5 (this is the same as 5000%). Look at this again, this is 0.5 x 100. It's not the same as one pink box.
When we convert our decimal of 0.5 to a percentage of 50% we should just have one pink box.
Can you see that multiplying by 100 doesn't work ?
Just looked up what my go-to trextbook (Rayner) says. It think the example below supports the multiply by 100 then attach the percentage sign. The order of operations is achieved with the brackets.
This example shows how to change three eighths to a percentage:
$$ \frac38 = ( \frac38 \times \frac{100}{1} ) \% = 37 \frac12 \%$$
So what do you think? Should we be teaching pupils to multiply by 100 or to multiply by 100% ?
If you are short of time you can answer a true/false question about this or leave a comment here.
An here's what the textbooks recommend. Click on the following small photograph to see a large sized photograph you can zoom in to:
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Please take a moment to share your opinion on this matter by clicking one of the buttons above.
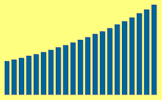
The following bar chart shows the proportions of people voting true and false so far.
|

|
| True | False |








PinusBanksianaSavage, Reddit
Wednesday, July 29, 2020
"If you must, think of percent as a unit and treat this as a unit conversion.
It's bad and sloppy to say 3/8=.375*100=37.5%, because where'd the percent sign come from? You are really multiplying by the unit conversion of 100%/1. So multiplying by 100% is technically correct and multiplying by 100 and then just appending the percent sign is sloppy."
FlamingBubba, Reddit
Wednesday, July 29, 2020
"It’s better to understand that that 1/4=25/100. If you are looking to convert 1/5, then 1/5=x/100. Cross multiply to solve. x=20, thus 20%."
Mrcorleymath, Reddit
Wednesday, July 29, 2020
"Fraction -> decimal -> x100 = percent"
Clive, Southampton
Wednesday, July 29, 2020
"If you multiply 0.35 by 100% on my calculator you don't get the 35% answer:
 "
"
Varaaki, Reddit
Wednesday, July 29, 2020
"Suggesting that 2/5 × 100 is equal to 40% is lunacy."
Ann Roberts,
Thursday, July 30, 2020
"You tell me that although your method isn't mathematically correct it gets the right answers every time.
Me: Mathematicians have a special way of describing methods that are mathematically incorrect.
You think for a while but you clearly haven't heard of it
Me: They call it 'Wrong'
Think about it.
Me: When does a Mathematician ever describe a method as mathematically incorrect and then proceed to use that method ?
Me: Imagine that NASA were offering you a free space flight to the moon and they told you that their calculations were mathematically incorrect. Would you take the flight ?
You have one last question for me.
Ok I can see that the formula is mathematically incorrect but it has been used by everyone for a long time and is giving them the right answers. They won't believe me that the formula is wrong. How can you explain that ?
Children have been shown that to convert a fraction to a percentage, you multiply by 100 and put a % sign on your answer. We call this the formula. This method is mathematically incorrect and I'm going to show you where the formula goes wrong.
Here's the truth:
Step One: Multiply by 100
2/5 x 100 = 40
Step Two: Divide both sides by 100
2/5 x 100/100 = 40/100
Check this on your calculator if you don't believe me.
If you combine Step One and Step Two, you have multiplied by 100 and divided by 100. This is the same as multiplying by 100%. I told you that the percentage sign is vital.
so when I combine Step One and Step Two, I have 2/5 x 100% = 40%.
We all agree that the answer is 40%.
If you told me to multiply by 100 and put a % sign on the answer, then you only told me some of the story. I'll highlight what you told me in red:
Step One: Multiply by 100
2/5 x 100 = 40 (which is equal to 4000%)
Step Two: Divide by 100
2/5 x 100/100 = 40/100
which can be stated as 2/5 x 100% = 40%
You didn't tell me about step two.
The formula is mathematically incorrect because it doesn't divide by 100. It misses out step two.
If you divide 40 by 100, you will have a mathematically correct answer of 40%.
And for one last time, you all ask me 'Does it really matter ?'
Yes it really does. It goes right back to the original question from the child:
If I convert 2/5 into an equivalent fraction, I multiply by one don't I ?
Yes I said.
so, I can multiply 2/5 by 20/20 to get 40/100 which is 40% ?
Yes, I said.
then they asked: but if I use the formula to convert a fraction to a percentage I have to multiply by 100 (the first part that I've shown in red). Why don't we multiply by the same amount ?
Clever child.
And one last thought, if it's ok to just put a % sign after a number and call it a percentage, then I'm going to put HRH after my name and call myself Queen of England.
What are you going to tell the Clever child ?"
The Clever Child, England
Thursday, July 30, 2020
"If the formula works, I could say that 2/5 x 100 = 40%
Let’s look at the Left Hand side 2/5 x 100 = 200/5 = 40
That’s plain old 40 without a percentage sign
Let’s look at the Right Hand Side. It’s 40%.
40% = 0.40
On that we can all agree
If the formula works then the LHS must equal the RHS
If the formula works, that would mean that 40 = 0.40
On that we can all disagree.
To convert a fraction to a percentage, you must multiply by 100%
and yes, multiplying by 100% is the same as multiplying by one."
Ann, England
Thursday, July 30, 2020
"Back to your formulas in the boxes:
We all agree that 100% = 100/100 = 1
0.35 x 100% is the same as 0.35 x 100/100
0.35 x 100/100 = 0.35/1 x 100/100
0.35/1 x 100/100 = 35/100 = 35%
This shows that 0.35 x 100% = 35%."
Ann Roberts,
Thursday, July 30, 2020
"Rayner is correct and he agrees with me.
 "
"
(3/8 x 100/1)% is the same as (3/8 x 100)%
x% means x/100
(3/8 x 100)% means (3/8 x 100)/100
(3/8 x 100)/100 = 3/8 x 100/100 Don't take my word for it. Try it on the calculator.
3/8 x 100/100 = 3/8 x 100% and this is what I said.
This bar model shows that 3/8 of 100% is 37.5%
Aamirmeyaji, Reddit
Friday, July 31, 2020
"I think it is intuitive if you understand the meaning of the word 'percent'. Percent means per-cent, which is per 100. (100 from cent, or century).
Therefore 100% = 100 * (1/100) = 1. So technically, to convert a fraction to percentage, you multiply it by 100%, which is essentially 1.
Let me know if this helped."
Tianavaig, Reddit
Friday, July 31, 2020
"You multiply by 100. But yeah....why?
The person in red has it right when they say: the calculation you have done gives you the answer I have highlighted in yellow. You have then had to multiply that number by 100 in your head to get the answer I have highlighted in green.
100% is not really a number as such, therefore you cannot exactly "multiply by 100%".
100% means "100 out of 100", or 100/100. Therefore, in decimal, 100% = 1.
The % sign is simply a symbol with a meaning. It means "out of one hundred" (literally, "per cent").
You can think of % as being equivalent to writing /100. So 25**%** is the same as 25**/100**.
Turning a fraction into a percentage is really just a case of finding the equivalent fraction which has 100 as the denominator (ie x/100). Then, you have an expression that can be read as "x out of 100" and, hey presto, there's your percentage.
If you're doing this by hand with "nice" numbers, it's just a case of fraction manipulation.
If you're using a calculator, that's where many people get confused about what multiplication to do.
When you type a division expression (e.g. 50/200) into a calculator, the calculator returns a decimal value. You could think of this as a fraction with 1 as the denominator.
e.g. type in 50/200 and you'll get 0.25. This could just as well be written 0.25/1. That's how your calculator works.
Now, remembering that percentages have 100 as the denominator, we need to get 100 on the bottom instead of 1. We achieve this by multiplying both top and bottom by 100.
So we get 50/200 = 0.25/1 = 25/100. Another way of writing 25/100 is 25% (note we are not involving the % symbol in the multiplication itself).
Shorthand, you could do (50/200)*100 = 25 And then we would write the answer as "25 out of 100" or 25%.
Sticking a % sign on the end is the same as saying "out of 100". It's just a piece of notation.
You may have noticed that I said "we need to multiply top and bottom by 100", and then I just did a single multiplication of 100 (ie multiplying the top). Sticking on a % sign is the same as multiplying the bottom by 100.
This is seen in the red box with the quote from the textbook. There's a x 100/1 inside the brackets, which multiplies the numerator by 100. So what about multiplying the denominator? That's taken care of by the % sign outside the bracket (remember that % is the same as /100).
At no point are we multiplying by %. We are simply using it as a piece of notation that has the equivalent meaning to /100."
The Clever Child, England
Friday, July 31, 2020
"Tell the world 1/5 x 100 > 20% because 20 > 0.20
Tell the world 0.30 x 100 > 30% because 30 > 0.30
Please tell the world to multiply by 100% when they convert fractions to percentages.
Please tell the world to multiply by 100% when they convert decimals to percentages.
1/5 x 100/100 = 100/500 = 20/100 = 20%
0.3 x 100/100 = 0.3/1 x 100/100 = 30/100 = 30%
Please tell the world."
Ann, England
Friday, July 31, 2020
"And don’t forget about the percentage change formula too.
Are you multiplying by 100 or 100% ?
The clever child says that you should multiply by 100%.
What did you decide ?"
JKlmn, Twitter
Friday, July 31, 2020
"These are all too formulaic which in my view is what is wrong with the way maths is often taught; Multiply by this, add that with no conceptual understanding. If children are taught a % is a special fraction with 100 as the denominator then they use equivalent fraction skills."
Ann, England
Friday, July 31, 2020
"Take a look at the formula to express an amount as a percentage of another amount.
Are you multiplying by 100 or 100% ?
What are you going to tell the clever child ?
He thinks you multiply by 100%."
Transum,
Friday, July 31, 2020
"I would teach the ‘make the denominator 100’ idea to pupils who did not have a good grasp of percentages. Thereafter I would encourage pupils to realise that a quick mental method is to multiply by 100 then append the percent sign. For written work, this would look like the Rayner example using brackets."
WeCanLearnAnything, Canada
Friday, July 31, 2020
"I wrote in-depth about converting between fractions and decimals. II discuss the tremendous amount of prior knowledge and nuance that can go into converting representations of rational numbers.
shorturl.at/lqEGS
In addition to everything in that post:
First, multiplying by 100 then slapping on a % symbol later is notationally sloppy, just like 2+3=5+1=6 is sloppy. It's a false statement that wrongly teaches students that the equals sign means "put the answer here" or "we're moving onto the next step" instead of "the left and right side of this mean the same thing".
Second, multiplying by 100% is correct and better, but, frankly, still weird. It just assumes the learner's knowledge of rational number arithmetic is VERY strong, which is quite unlikely. It also, in the eyes of a student, seems to come out of nowhere how is it similar to any prior math they've ever done?
Third, here are two ways to convert fractions to percents, but they require prior knowledge not addressed in this thread. See the link above. They also require students to know that "percent" and "hundredth" are synonyms the same way "dozen" and "twelve" are synonyms.
Method 1: With Friendly Numbers, Use Equivalent Fractions
Example: 4/5 = 80/100 = 80%
Example: 5/4 = 125/100 = 125%
Example: 46/200 = 23/100 = 23%
In practice, you should provide visuals for these and ensure explicit understanding that this is almost exactly like prior work they've done with equivalent fractions
Method 2: With Less Friendly Numbers, Treat Fractions Like a Quotient, Then Apply Base 10 Knowledge
Example: 3/8 = 3÷8 = 0.125 = 1/10 + 2/100 + 5/1000 = 10/100 + 2/100 + 0.5/100 = 12.5/100 = 12.5%
Example: 10/7 = 10÷7 ? 1.4286 = 1 + 4/10 + 2/100 + 8/1000 + 6/10000 = 100/100 + 40/100 + 2/100 + 0.8/100 + 0.06/100 = 142.86/100 = 142.86%
In practice, many students do not know why a fraction is a quotient, so make sure you teach that first!"
Ann, England
Friday, July 31, 2020
"The mental maths method works like this:
Step One: Multiply by 100
3/8 x 100
Step Two: Now append a % sign
(3/8 x 100)%
And you get
(3/8 x 100)% = 37.5%
This agrees with Rayner and the Clever Child likes this method.
If you use the dodgy formula, you would be appending the % sign in the wrong place like this:
Step One: Multiply by 100
3/8 x 100 = 37.5
Step Two: Append the % sign
3/8 x 100 = 37.5% This isn't mathematically correct and that’s why the clever child was confused.
Please make sure you append the % sign in the right place."
WeCanLearnAnything, Canada
Friday, July 31, 2020
"@Clive
When looking at 0.35, what does that, by base 10 convention, actually MEAN?
0.35
= 0.3 + 0.05
= 3/10 + 5/100
= 30/100 + 5/100
= 35/100
= 35%
0.35 and 35% mean exactly the same thing.
Your calculator, though, did this:
0.35 x 100%
= 0.35 x 100(1/100)
= 0.35 x 100/100
= 0.35 x 1
= 0.35."
Sean K And Jo Morgan, Twitter
Saturday, August 1, 2020
Robert Low, Twitter
Saturday, August 1, 2020
David Butler, Twitter
Saturday, August 1, 2020
"
Vic, Gunstone
Saturday, August 1, 2020
"Have you ever taught calculus? Did you first teach differentiation from first principles then the ‘trick’ or quick algorithm for differentiating polynomials?
Can you see the connection?
I believe we first teach for understanding then we help pupils develop ‘shortcuts’ for mental calculations. I don’t think ‘multiply by 100’ is so bad.
Close your eyes, I will ask you a question: “What is 0.45 as a percentage? … Boom you did it… you just multiplied 0.45 by a hundred didn’t you? "
Ann, England
Sunday, August 2, 2020
"Replying to Vic, Gunstone
What if I said that I multiply by 100 in my head too ?
I bet nobody expected me to say that.
Let's consider the example of converting 0.45 to the percentage 45%
The debate is about which of these statements I can WRITE as my answer:
0.45 x 100% = 45% YES,correct
or 0.45 x 100 = 45% NO,wrong
Teachers should mark the last statement as wrong because:
0.45 x 100 = 45
45% = 0.45
so 0.45 x 100 > 45%
The mathematically correct statement will be 0.45 x 100% = 45%
Which of these statements will you write as your answer ?"